Question

關于x的實系數方程x²+ax+2b=0的一根在（0，1）內，另一根在（1，2）內，則點（a，b）所在區域的面積為    ．

Answer 1

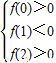
【答案】分析：設f（x）=x²+ax+2b，則有成立，畫出滿足約束條件的可行域，即可求出面積．
解答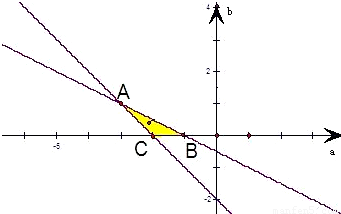：解：設f（x）=x²+ax+2b，由題意得：
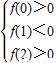
，即，
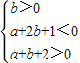
在坐標系aOb中畫出上述不等式組表示的平面區域，
由題意，約束條件表示的平面區域為陰影部分（不包括邊界）．其中A（-3，1），B（-1，0），C（-2，0）
根據平面區域，易求得點（a，b）所在區域的面積為==．
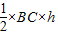
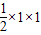
故答案為：．
點評：本題主要考查了簡單的線性規劃，函數零點的判定定理，以及利用幾何意義求面積，屬于基礎題．