
分析 (1)由實部lg(m2-2m-2)=0,且虛部(m2+3m+2)≠0,求得m的值即可;
(2)由復數的虛部m2+3m+2=0 且m2-2m-2>0時,求得m的值即可;
(3)由實部lg(m2-2m-2)>0,且虛部(m2+3m+2)<0時,求得m值即可.
解答 解:(1)若z是純虛數,
則$\left\{\begin{array}{l}{{m}^{2}-2m-2=1}\\{{m}^{2}+3m+2≠0}\end{array}\right.$,
解得m=3.
故m=3時,z為純虛數;
(2)若z是實數,
則$\left\{\begin{array}{l}{{m}^{2}-2m-2>0}\\{{m}^{2}+3m+2=0}\end{array}\right.$,
解得m=-2或-1.
故m=-2或-1時,z是實數;
(3)若z對應的點在復平面的第四象限,
則lg(m2-2m-2)>0,且(m2+3m+2)<0,
解得 m<-1或m>3,
故當m<-1或m>3時,復數對應的點位于復平面的第四象限.
點評 本題考查了復數的基本概念,一元二次不等式、對數不等式的解法,屬于中檔題.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ③④ | C. | ③ | D. | ①④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
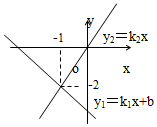 如圖所示,兩函數y1=k1x+b和y2=k2x的圖象相交于點(-1,-2),則關于x的不等式 k1x+b>k2x的解集為( )
如圖所示,兩函數y1=k1x+b和y2=k2x的圖象相交于點(-1,-2),則關于x的不等式 k1x+b>k2x的解集為( )| A. | x>-1 | B. | x<-1 | C. | x<-2 | D. | 無法確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $t=\frac{1}{2}$ | B. | t=1 | C. | t=2 | D. | t=3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com