
分析 (Ⅰ)按照極值點在區間[m,m+1](m>0)的右側、內部、左側三種情況進行討論,由函數的單調性即可求得其最小值;
(Ⅱ)依據指數函數y=ex與對數函數y=lnx關于直線y=x對稱的特征,得到過原點的切線也關于直線y=x對稱,主要考查利用導函數研究曲線的切線及結合方程有解零點存在定理的應該用求參數的問題,得到不等式的證明;
解答 (Ⅰ)解:$t(x)=\frac{e^x}{x},x∈(0,+∞)$,$t'(x)=\frac{{x{e^x}-{e^x}}}{x^2}$…(1分)
令t'(x)>0得x>1,令t'(x)<0得x<1,
所以,函數t(x)在(0,1)上是減函數,在(1,+∞)上是增函數,…(3分)
∴當m≥1時,t(x)在[m,m+1](m>0)上是增函數,∴$t{(x)_{min}}=t(m)=\frac{e^m}{m}$…(4分)
當0<m<1時,函數t(x)在[m,1]上是減函數,在[1,m+1]上是增函數,
∴t(x)min=t(1)=e.…(5分)
(Ⅱ)設l2的方程為y=k2x,切點為(x2,y2),則${y_2}={e^{x_2}}$,${k_2}=g'({x_2})={e^{x_2}}=\frac{y_2}{x_2}$
∴x2=1,y2=e∴k2=e.…(6分)
由題意知,切線l1的斜率${k_1}=\frac{1}{k_2}=\frac{1}{e}$,∴切線l1的方程為$y=\frac{1}{e}x$,設l1與曲線y=f(x)的切點為(x1,y1),∴${k_1}=f'({x_1})=\frac{1}{x_1}-a=\frac{1}{e}=\frac{y_1}{x_1}$,∴${y_1}=\frac{x_1}{e}=1-a{x_1}$,$a=\frac{1}{x_1}-\frac{1}{e}$,
又y1=lnx1-a(x1-1),消去y1,a后整理得$ln{x_1}-1+\frac{1}{x_1}-\frac{1}{e}=0$,$a=\frac{1}{x_1}-\frac{1}{e}$…(8分)
令$m(x)=lnx-1+\frac{1}{x}-\frac{1}{e}$,則$m'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,
∴m(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增,…(9分)
若x1∈(0,1),∵$m(\frac{1}{e})=-2+e-\frac{1}{e}>0$,$m(1)=-\frac{1}{e}<0$,∴${x_1}∈(\frac{1}{e},1)$,
而$a=\frac{1}{x_1}-\frac{1}{e}$,在$(\frac{1}{e},1)$單調遞減,∴$\frac{e-1}{e}<a<\frac{{{e^2}-1}}{e}$. …(10分)
若x1∈(1,+∞),∵m(x)在(1,+∞)上單調遞增,且m(e)=0,
∴x1=e,∴$a=\frac{1}{x_1}-\frac{1}{e}=0$…(11分)
綜上,a=0或$\frac{e-1}{e}<a<\frac{{{e^2}-1}}{e}$.…(12分)
點評 本題考查利用導數討論含參數函數的單調性及最值、利用導數求曲線的切線問題,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分別 是PC,PD,BC的中點.
如圖,在四棱錐P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分別 是PC,PD,BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
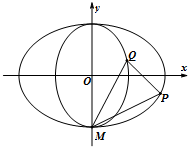 如圖,中心在坐標原點,焦點分別在x軸和y軸上的橢圓T1,T2都過點M(0,-$\sqrt{2}$),且橢圓T1與T2的離心率均為$\frac{\sqrt{2}}{2}$.
如圖,中心在坐標原點,焦點分別在x軸和y軸上的橢圓T1,T2都過點M(0,-$\sqrt{2}$),且橢圓T1與T2的離心率均為$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
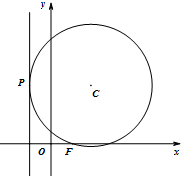 如圖,動圓C過點F(1,0),且與直線x=-1相切于點P.
如圖,動圓C過點F(1,0),且與直線x=-1相切于點P.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com