
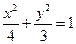 的左、右焦點,曲線C是坐標原點為頂
的左、右焦點,曲線C是坐標原點為頂 點,
點, 以F2為焦點的拋物線,過點F1的直線
以F2為焦點的拋物線,過點F1的直線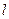 交曲線C于x軸上方兩個不同點P、Q,點P關(guān)于x軸的對稱點為M,設(shè)
交曲線C于x軸上方兩個不同點P、Q,點P關(guān)于x軸的對稱點為M,設(shè)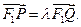
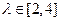 ,求直線
,求直線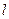 的斜率k的取值范圍;
的斜率k的取值范圍; 開心練習(xí)課課練與單元檢測系列答案
開心練習(xí)課課練與單元檢測系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
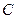 :
: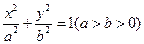 ,
,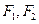 為其左、右焦點,
為其左、右焦點,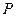 為橢圓
為橢圓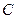 上任一點,
上任一點,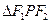 的重心為
的重心為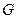 ,內(nèi)心
,內(nèi)心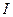 ,且有
,且有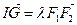 (其中
(其中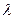 為實數(shù))
為實數(shù))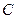 的離心率
的離心率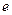 ;
;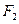 的直線
的直線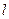 與橢圓
與橢圓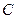 相交于點
相交于點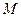 、
、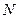 ,若
,若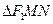 面積的最大值為3,求橢圓
面積的最大值為3,求橢圓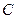 的方程.
的方程.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
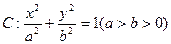 的兩個焦點F1、F2,點P在橢圓C上,且PF1⊥F1F2,且|PF1|=
的兩個焦點F1、F2,點P在橢圓C上,且PF1⊥F1F2,且|PF1|=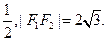
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 短軸
短軸 的一個端點
的一個端點 ,離心率
,離心率 .過
.過 作直線
作直線 與橢圓交于另一點
與橢圓交于另一點 ,與
,與 軸交于點
軸交于點 (
( 不同于原點
不同于原點 ),點
),點 關(guān)于
關(guān)于 軸的對稱點為
軸的對稱點為 ,直線
,直線 交
交 軸于點
軸于點 .
. 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
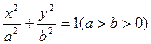 經(jīng)過點
經(jīng)過點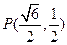 ,離心率為
,離心率為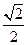 ,動點
,動點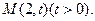
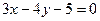 截得的弦長為2的圓的方程;
截得的弦長為2的圓的方程;查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com