
【題目】正方體![]() 的棱長為1,
的棱長為1,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,過直線
的中點,過直線![]() 的平面分別與棱
的平面分別與棱![]() 、
、![]() 交于
交于![]() ,設
,設![]() ,
,![]() ,給出以下四個命題:
,給出以下四個命題:
①四邊形![]() 為平行四邊形;
為平行四邊形;
②若四邊形![]() 面積
面積![]() ,
,![]() ,則
,則![]() 有最小值;
有最小值;
③若四棱錐![]() 的體積
的體積![]()
![]() ,
,![]() ,則
,則![]() 為常函數;
為常函數;
④若多面體![]() 的體積
的體積![]() ,
,![]() ,則
,則![]() 為單調函數.
為單調函數.
其中假命題為( )
A.① ③ B.② C.③④ D.④
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() ,若函數
,若函數![]() 的圖象與x軸的任意兩個相鄰交點間的距離為
的圖象與x軸的任意兩個相鄰交點間的距離為![]() ,當
,當![]() 時,函數
時,函數![]() 取得最大值
取得最大值![]() .
.
(1)求函數![]() 的解析式,并寫出它的單調增區間;
的解析式,并寫出它的單調增區間;
(2)若![]() ,求函數
,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() ,三個函數的定義域均為集合
,三個函數的定義域均為集合![]() .
.
(1)若![]() ,試判斷集合
,試判斷集合![]() 與
與![]() 的關系,并說明理由;
的關系,并說明理由;
(2)記![]() ,是否存在
,是否存在![]() ,使得對任意的實數
,使得對任意的實數![]() ,函數
,函數![]() 有且僅有兩個零點?若存在,求出滿足條件的最小正整數
有且僅有兩個零點?若存在,求出滿足條件的最小正整數![]() ;若不存在,說明理由.(以下數據供參考:
;若不存在,說明理由.(以下數據供參考:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】口袋中裝有質地大小完全相同的5個球,編號分別為1,2,3,4,5,甲、乙兩人玩一種游戲:甲先摸一個球,記下編號,放回后乙再摸一個球,記下編號.如果兩個編號的和為偶數就算甲勝,否則算乙勝.
(1)求甲勝且編號的和為6的事件發生的概率;
(2)這種游戲規則公平嗎?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某動物園要建造兩間完全相同的矩形熊貓居室,其總面積為24平方米,設熊貓居室的一面墻![]() 長為
長為![]() 米(2
米(2![]() ).
).
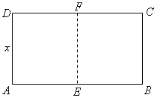
⑴用![]() 表示墻
表示墻![]() 的長;
的長;
⑵假設所建熊貓居室的墻壁造價(在墻壁高度一定的前提下)為每米1000元,請將墻壁的總造價![]() (元)表示為
(元)表示為![]() (米)的函數;
(米)的函數;
⑶當![]() 為何值時,墻壁的總造價最低?
為何值時,墻壁的總造價最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,GH是東西方向的公路北側的邊緣線,某公司準備在GH上的一點B的正北方向的A處建設一倉庫,設![]() ,并在公路北側建造邊長為
,并在公路北側建造邊長為![]() 的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且
的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 關于
關于![]() 的函數解析式,并求出定義域;
的函數解析式,并求出定義域;
(2)如果中轉站四堵圍墻造價為10萬元/km,兩條道路造價為30萬元/km,問:![]() 取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.
取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com