
 .
.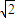 .
.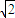 .
.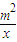 -2m.
-2m.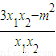 )
)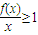 恒成立∴f(x)≥x恒成立,
恒成立∴f(x)≥x恒成立,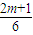 <1
<1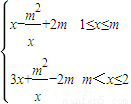
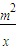 +m在[1,m]為遞增,
+m在[1,m]為遞增,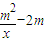 在[m,2]為遞增,
在[m,2]為遞增,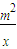 +2m(無解)
+2m(無解)

 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省南京市高考數學3月信息試卷(解析版) 題型:解答題
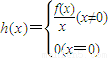 .
.查看答案和解析>>
科目:高中數學 來源:2010年高三數學二輪沖刺練習試卷(07)(解析版) 題型:解答題
 .
.查看答案和解析>>
科目:高中數學 來源:2012-2013學年河南省十所名校高三第三次聯考文科數學試卷(解析版) 題型:解答題
設m為實數,函數f(x)=- +2x+m,x∈R
+2x+m,x∈R
(Ⅰ)求f(x)的單調區間與極值;
(Ⅱ)求證:當m≤1且x>0時, >2
>2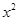 +2mx+1.
+2mx+1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com