
某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔一小時抽一件產品,稱其質量(單位:克)是否合格,分別記錄抽查數據,獲得質量數據莖葉圖如圖,則 車間的產品的質量相對穩定;若從乙車間6件樣品中隨機抽取兩件,則所抽取兩件樣品質量之差不超過2克的概率為 .
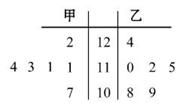
【解析】①設甲、乙兩個車間產品質量的平均值分別為![]() ,
,![]() ,方差分別為
,方差分別為![]() ,
,![]() ,
,
則![]() =
=![]() =113,
=113,
![]() =
=![]() =113,
=113,
![]() =
=![]() ×[(122-113)2+(114-113)2+(113-113)2+(111-113)2+ (111-113)2+(107-113)2]=21,
×[(122-113)2+(114-113)2+(113-113)2+(111-113)2+ (111-113)2+(107-113)2]=21,
![]() =
=![]() ×[(124-113)2+(110-113)2+(112-113)2+(115-113)2+ (108-113)2+(109-113)2]=29.33,
×[(124-113)2+(110-113)2+(112-113)2+(115-113)2+ (108-113)2+(109-113)2]=29.33,
由于![]() <
<![]() ,所以甲車間的產品的質量相對穩定.
,所以甲車間的產品的質量相對穩定.
②從乙車間6件樣品中隨機抽取兩件,結果共有15個:
(124,110),(124,112),(124,115),(124,108),(124,109),(110,112),
(110,115),(110,108),(110,109),(112,115),(112,108),(112,109),
(115,108),(115,109),(108,109).
設所抽取兩件樣品質量之差不超過2克的事件為A,則事件A共有4個結果:
(110,112),(110,108),(110,109),(108,109).
![]() 所以P(A)=
所以P(A)=![]() .
.
答案:甲 ![]()


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
 某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔1小時抽一包產品,稱其重量(單位:克)是否合格,分別記錄抽查數據,獲得重量數據的莖葉圖如圖.
某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔1小時抽一包產品,稱其重量(單位:克)是否合格,分別記錄抽查數據,獲得重量數據的莖葉圖如圖.查看答案和解析>>
科目:高中數學 來源: 題型:
甲車間:102,101,99,103,98,99,98;
乙車間:110,115,90,85,75,115,110.
估計甲、乙兩車間的均值與方差,并說明哪個車間產品較穩定.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省中山市實驗高中高三11月階段考試文科數學試卷(解析版) 題型:解答題
某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔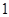 小時抽一包產品,稱其重量(單位:克)是否合格,分別記錄抽查數據,獲得重量數據的莖葉圖如圖所示.
小時抽一包產品,稱其重量(單位:克)是否合格,分別記錄抽查數據,獲得重量數據的莖葉圖如圖所示.
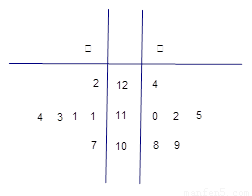
(1)根據樣品數據,計算甲、乙兩個車間產品重量的平均值與方差,并說明哪個車間的產品的重量相對較穩定;
(2)若從乙車間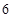 件樣品中隨機抽取兩件,求所抽取的兩件樣品的重量之差不超過
件樣品中隨機抽取兩件,求所抽取的兩件樣品的重量之差不超過 克的概率.
克的概率.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省漳州市高三適應性檢測文科數學試卷(解析版) 題型:解答題
某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔1小時抽一包產品,稱其重量(單位:克)是否合格,分別記錄了6個抽查數據,獲得重量數據的莖葉圖如圖4.
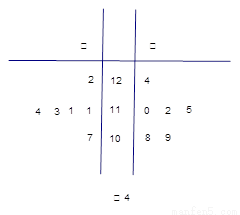
(1) 根據樣品數據,計算甲、乙兩個車間產品重量的均值與方差,并說明哪個車間的產品的重量相對較穩定;
(2) 若從乙車間6件樣品中隨機抽取兩件,求所抽取的兩件樣品的重量之差不超過2克的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com