
幾何證明選講如圖:已知圓上的弧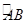 =
=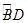 ,過C點的圓的切線與BA的延長線交于E點
,過C點的圓的切線與BA的延長線交于E點
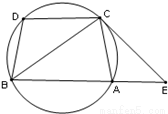
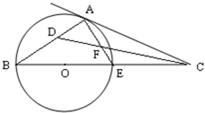
證明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC2=BE×CD.
由同圓中等圓弧的性質可得∠ABC=∠BCD.由弦切角定理可得∠ACE=∠ABC,即可得出證明.(II)利用弦切角定理可得∠CDB=∠BCE,由相似三角形的判定定理可得△BEC∽△CBD,由相似三角形的性質可得BC2=BE×CD.,即可求出BC
【解析】
試題分析:解:(Ⅰ)因為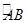 =
=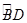 ,
,
所以∠BCD=∠ABC.
又因為EC與圓相切于點C,
故∠ACE=∠ABC
所以∠ACE=∠BCD.(5分)
(Ⅱ)因為∠ECB=∠CDB,∠EBC=∠BCD,
所以△BDC~△ECB,
故BC:BE="CD:BC" .
即BC2=BE×CD.(10分)
考點:同圓中等圓弧的性質
點評:熟練掌握同圓中等圓弧的性質、弦切角定理、相似三角形的判定和性質定理是解題的關鍵.


科目:高中數學 來源: 題型:
 選修4-1:幾何證明選講
選修4-1:幾何證明選講查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•宿遷一模)【選做題】本題包括A、B、C、D四小題,請選定其中兩題,并在相應的答題區域內作答.若多做,則按作答的前兩題評分.解答時應寫出文字說明、證明過程或演算步驟.
(2013•宿遷一模)【選做題】本題包括A、B、C、D四小題,請選定其中兩題,并在相應的答題區域內作答.若多做,則按作答的前兩題評分.解答時應寫出文字說明、證明過程或演算步驟.| 5 |
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 |
| AC |
 |
| BD |
查看答案和解析>>
科目:高中數學 來源: 題型:
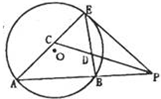 (2012•洛陽模擬)選修4-1:幾何證明選講
(2012•洛陽模擬)選修4-1:幾何證明選講| CA |
| CE |
| PE |
| PB |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com