
【題目】已知函數![]() ,
, ![]()
(1)若兩函數圖象有兩個不同的公共點,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,
, ![]() ,求實數
,求實數![]() 的最大值.
的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(1)由兩函數圖象有兩個不同的公共點可等價于方程![]() 在
在![]() 有兩個不同的解,即方程
有兩個不同的解,即方程![]() 在
在![]() 有兩個不同的解,設
有兩個不同的解,設![]() ,求導的函數
,求導的函數![]() 的單調性,從而求出
的單調性,從而求出![]() 的最大值,從而可求出實數
的最大值,從而可求出實數![]() 的取值范圍;(2)由
的取值范圍;(2)由![]() 在
在![]() 上恒成立,等價于
上恒成立,等價于![]() 對
對![]() 恒成立,設
恒成立,設![]() ,則只需
,則只需![]() ,對
,對![]() 求導分析其單調性,從而可得
求導分析其單調性,從而可得![]() ,即可得到實數
,即可得到實數![]() 的最大值.
的最大值.
試題解析:(1)解:函數![]() 與
與![]() 的圖象有兩個不同的公共點等價于方程
的圖象有兩個不同的公共點等價于方程![]() 在
在![]() 有兩個不同的解,即方程
有兩個不同的解,即方程![]() 在
在![]() 有兩個不同的解.
有兩個不同的解.
設![]() ,則函數
,則函數![]() 的圖象與直線
的圖象與直線![]() 有兩個不同的交點.
有兩個不同的交點.
由![]() ,令
,令![]() ,有
,有![]() .
.
列表如下:
|
|
|
|
| + | 0 | - |
| 增函數 | 極大值 | 減函數 |
∴函數有極大值![]()
∵![]() 時,
時, ![]() ;
; ![]() ,
, ![]()
∴![]()
(注:或①當![]() 時,至多有一個公共點;②當
時,至多有一個公共點;②當![]() 時,因為
時,因為![]() 時,
時, ![]() , 至多有一個公共點;③當
, 至多有一個公共點;③當![]() 時,因為
時,因為![]() ,
, ![]() ,所以
,所以![]() 上有一個零點,又
上有一個零點,又![]() ,而
,而![]() ,所以在
,所以在![]() 上存在一個零點,即
上存在一個零點,即![]() 時,有兩個零點)
時,有兩個零點)
(2)由題![]() 對
對![]() 恒成立,即
恒成立,即![]() 對
對![]() 恒成立,即
恒成立,即![]() 對
對![]() 恒成立,
恒成立,
設![]() ,則只需
,則只需![]() ,由
,由![]() ,
,
又∵![]()
∴![]() 在
在![]() 為增函數
為增函數
∴![]()
又∵![]()
∴存在![]() 使
使![]() ,即
,即![]() ,則
,則![]()
又∵![]() 時,
時, ![]() ,
, ![]() 為減函數,
為減函數, ![]() 時,
時, ![]() ,
, ![]() 為增函數
為增函數
∴
∴![]() 在
在![]() 為增函數
為增函數
∴![]()
![]()
![]()
∴![]() ,故實數
,故實數![]() 的最大值為
的最大值為![]() .
.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,|an+1-an|=pn,n∈N*.
(1)若{an}是遞增數列,且a1,2a2,3a3成等差數列,求p的值;
(2)若p=,且{a2n-1}是遞增數列,{a2n}是遞減數列,求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x+1)e-x(e為自然對數的底數).
(1)求函數f(x)的單調區間;
(2)設函數φ(x)=xf(x)+tf′(x)+e-x,存在實數x1,x2∈[0,1],使得2φ(x1)<φ(x2)成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已經函數![]() 的定義域為
的定義域為![]() ,設
,設![]()
(1)試確定![]() 的取值范圍,使得函數
的取值范圍,使得函數![]() 在
在![]() 上為單調函數
上為單調函數
(2)求證![]()
(3)若不等式![]() (為
(為![]() 正整數)對任意正實數
正整數)對任意正實數![]() 恒成立,求
恒成立,求![]() 的最大值.(解答過程可參考使用以下數據
的最大值.(解答過程可參考使用以下數據![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把2支相同的晨光簽字筆,3支相同英雄鋼筆全部分給4名優秀學生,每名學生至少1支,則不同的分法有( )
A. 24種 B. 28種 C. 32種 D. 36種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第三屆移動互聯創新大賽,于2017年3月~10月期間舉行,為了選出優秀選手,某高校先在計算機科學系選出一種子選手![]() ,再從全校征集出3位志愿者分別與
,再從全校征集出3位志愿者分別與![]() 進行一場技術對抗賽,根據以往經驗,
進行一場技術對抗賽,根據以往經驗, ![]() 與這三位志愿者進行比賽一場獲勝的概率分別為
與這三位志愿者進行比賽一場獲勝的概率分別為![]() ,且各場輸贏互不影響.
,且各場輸贏互不影響.
(1)求甲恰好獲勝兩場的概率;
(2)求甲獲勝場數的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() ,點
,點![]() 是圓上一動點,
是圓上一動點, ![]() 的垂直平分線與線段
的垂直平分線與線段![]() 交于點
交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 且斜率不為0的直線
且斜率不為0的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,證明直線
,證明直線![]() 過定點,并求
過定點,并求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著科學技術的飛速發展,手機的功能逐漸強大,很大程度上代替了電腦、電視.為了了解某高校學生平均每天使用手機的時間是否與性別有關,某調查小組隨機抽取了![]() 名男生、
名男生、![]() 名女生進行為期一周的跟蹤調查,調查結果如表所示:
名女生進行為期一周的跟蹤調查,調查結果如表所示:
平均每天使用手機超過 | 平均每天使用手機不超過 | 合計 | |
男生 |
|
|
|
女生 |
|
|
|
合計 |
|
|
|
(1)能否在犯錯誤的概率不超過![]() 的前提下認為學生使用手機的時間長短與性別有關?
的前提下認為學生使用手機的時間長短與性別有關?
(2)在這![]() 名女生中,調查小組發現共有
名女生中,調查小組發現共有![]() 人使用國產手機,在這
人使用國產手機,在這![]() 人中,平均每天使用手機不超過
人中,平均每天使用手機不超過![]() 小時的共有
小時的共有![]() 人.從平均每天使用手機超過
人.從平均每天使用手機超過![]() 小時的女生中任意選取
小時的女生中任意選取![]() 人,求這
人,求這![]() 人中使用非國產手機的人數
人中使用非國產手機的人數![]() 的分布列和數學期望.
的分布列和數學期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: 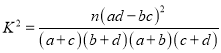
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com