【題目】某地區2007年至2013年農村居民家庭純收入y（單位：千元）的數據如下表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求y關于t的線性回歸方程；
（2）利用（1）中的回歸方程，分析2007年至2013年該地區農村居民家庭人均純收入的變化情況，并預測該地區2015年農村居民家庭人均純收入.
附：回歸直線的斜率和截距的最小二乘法估計公式分別為：
，
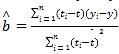【答案】（1）
；（2）在2007至2013年該地區農村居民家庭人均純收入在逐年增加，平均每年增加
千元；
元.
【解析】試題本題第（1）問，由給出的
與
公式求出與，從而求出回歸直線方程；對第（2）問，由第（1）問求出的回歸直線方程進行預測，令
，可得
的近似值.
試題解析：（1）由題意知，
，
，所以
=，
所以
=
=
，所以線性回歸方程為。
（2）由（1）中的線性回歸方程可知，
，所以在2007至2013年該地區農村居民家庭人均純收入在逐年增加，平均每年增加千元.
令得：
，故預測該地區在2015年農村居民家庭人均純收入為元。
【易錯點】本題的易錯點是第（1）問計算錯誤，第（2）問在2007至2013年該地區農村居民家庭人均純收入的變化情況，不知道如何回答.
科目：高中數學 來源： 題型：
【題目】已知拋物線
：
.
（1）若直線
經過拋物線的焦點，求拋物線的準線方程；
（2）若斜率為-1的直線經過拋物線的焦點
，且與拋物線交于
，
兩點，當
時，求拋物線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為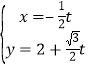
(
為參數)，以原點為極點，以
軸的正半軸為極軸，建立極坐標系，曲線
的極坐標方程為
，
(Ⅰ)求曲線的普通方程和曲線的直角坐標方程；
(Ⅱ)設點
，曲線與曲線交于
兩點，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
是雙曲線
上一點， 
分別是雙曲線
的左、右頂點，直線
的斜率之積為
.
(1)求雙曲線的離心率；
(2)過雙曲線
的右焦點且斜率為
的直線交雙曲線于
兩點， 
為坐標原點， 
為雙曲線上一點，滿足
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，AB//CD，且
.
（1）證明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC， 
，求二面角A-PB-C的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】即將于
年夏季畢業的某大學生準備到貴州非私營單位求職，為了了解工資待遇情況，他在貴州省統計局的官網上，查詢到
年到
年非私營單位在崗職工的年平均工資近似值（單位：萬元），如下表：
年份 |
|
|
|
|
|
|
|
|
|
|
序號 |
|
|
|
|
|
|
|
|
|
|
年平均工資 |
|
|
|
|
|
|
|
|
|
|
（1）請根據上表的數據，利用線性回歸模型擬合思想，求
關于
的線性回歸方程
（
，
的計算結果根據四舍五入精確到小數點后第二位）；
（2）如果畢業生對年平均工資的期望值為8.5萬元，請利用（1）的結論，預測年的非私營單位在崗職工的年平均工資（單位：萬元。計算結果根據四舍五入精確到小數點后第二位），并判斷年平均工資能否達到他的期望.
參考數據：
，
，
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附：對于一組具有線性相關的數據：
，
，
，
，
其回歸直線的斜率和截距的最小二乘法估計分別為
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
，
為橢圓的左、右焦點，點
在直線
上且不在
軸上，直線
與橢圓的交點分別為
和
，
為坐標原點.
設直線的斜率為
，證明：
問直線
上是否存在點，使得直線
的斜率
滿足
？若存在，求出所有滿足條件的點的坐標；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設有下列四個命題：
：若
，則
；
：若
，則
；
：“
”是“
為奇函數”的充要條件；
：“等比數列
中，
”是“等比數列是遞減數列”的充要條件．
其中，真命題的是
A. ，
B. ，C. ，
D. ，
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
