
【題目】已知命題p:存在x0∈R,使![]() ;命題q:對任意x∈R,mx2+mx+1>0;若p∨q為真,p∧q為假,求實數m的取值范圍.
;命題q:對任意x∈R,mx2+mx+1>0;若p∨q為真,p∧q為假,求實數m的取值范圍.
 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】![]() 是空氣質量的一個重要指標,我國
是空氣質量的一個重要指標,我國![]() 標準采用世衛組織設定的最寬限值,即
標準采用世衛組織設定的最寬限值,即![]() 日均值在
日均值在![]() 以下空氣質量為一級,在
以下空氣質量為一級,在![]() 之間空氣質量為二級,在
之間空氣質量為二級,在![]() 以上空氣質量為超標.如圖是某地
以上空氣質量為超標.如圖是某地![]() 月
月![]() 日到
日到![]() 日
日![]() 日均值(單位:
日均值(單位:![]() )的統計數據,則下列敘述不正確的是( )
)的統計數據,則下列敘述不正確的是( )
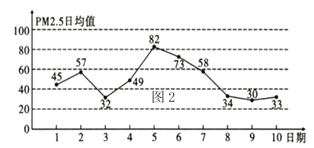
A.從![]() 日到
日到![]() 日,
日,![]() 日均值逐漸降低
日均值逐漸降低
B.這![]() 天的
天的![]() 日均值的中位數是
日均值的中位數是![]()
C.這![]() 天中
天中![]() 日均值的平均數是
日均值的平均數是![]()
D.從這![]() 天的日均
天的日均![]() 監測數據中隨機抽出一天的數據,空氣質量為一級的概率是
監測數據中隨機抽出一天的數據,空氣質量為一級的概率是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知過點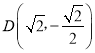 的橢圓
的橢圓![]() 的離心率為
的離心率為![]() ,左頂點和上頂點分別為A,B.
,左頂點和上頂點分別為A,B.
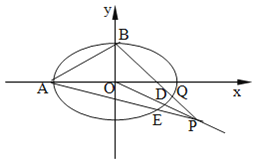
(1)求橢圓的標準方程;
(2)若P為線段OD延長線上一點,直線PA交橢圓于另一點E,直線PB交橢圓于另一點Q.
①求直線PA與PB的斜率之積;
②判斷直線AB與EQ是否平行?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們知道,地球上的水資源有限,愛護地球、節約用水是我們每個人的義務和責任.某市政府為了對自來水的使用進行科學管理,節約水資源,計劃確定一個家庭年用水量的標準,為此,對全市家庭日常用水的情況進行抽樣調查,并獲得了![]() 個家庭某年的用水量(單位:立方米),統計結果如下表所示.
個家庭某年的用水量(單位:立方米),統計結果如下表所示.
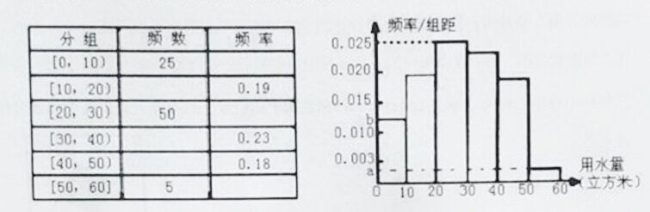
(Ⅰ)分別求出![]() 的值;
的值;
(Ⅱ)若以各組區間中點值代表該組的取值,試估計全市家庭平均用水量;
(Ⅲ)從樣本中年用水量在![]() (單位:立方米)的
(單位:立方米)的![]() 個家庭中任選
個家庭中任選![]() 個,作進一步跟蹤研究,求年用水量最多的家庭被選中的概率(
個,作進一步跟蹤研究,求年用水量最多的家庭被選中的概率(![]() 個家庭的年用水量都不相等).
個家庭的年用水量都不相等).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,以
為極點,以![]() 軸為非負半軸為極軸建立極坐標系,兩坐標系相同的長度單位.圓
軸為非負半軸為極軸建立極坐標系,兩坐標系相同的長度單位.圓![]() 的方程為
的方程為![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)設圓![]() 與直線
與直線![]() 交于點
交于點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動圓M與圓F1:x2+y2+6x+5=0外切,同時與圓F2:x2+y2﹣6x﹣91=0內切.
(1)求動圓圓心M的軌跡方程E,并說明它是什么曲線;
(2)若直線y![]() x+m與(1)中的軌跡E有兩個不同的交點,求m的取值范圍.
x+m與(1)中的軌跡E有兩個不同的交點,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一顆骰子先后拋擲2次,觀察向上的點數.
(1) 列舉出所有可能的結果,并求兩點數之和為5的概率;
(2) 求以第一次向上點數為橫坐標x,第二次向上的點數為縱坐標y的點![]() 在圓
在圓![]() 的內部的概率.
的內部的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極坐標建立極坐標系,圓
軸正半軸為極坐標建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
![]() 求
求![]() 的普通方程;
的普通方程;
![]() 將圓
將圓![]() 平移,使其圓心為
平移,使其圓心為![]() ,設
,設![]() 是圓
是圓![]() 上的動點,點
上的動點,點![]() 與
與![]() 關于原點
關于原點![]() 對稱,線段
對稱,線段![]() 的垂直平分線與
的垂直平分線與![]() 相交于點
相交于點![]() ,求
,求![]() 的軌跡的參數方程.
的軌跡的參數方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M的方程為x2+y2-2x-2y-6=0,以坐標原點O為圓心的圓O與圓M相切.
(1)求圓O的方程;
(2)圓O與x軸交于E,F兩點,圓O內的動點D使得DE,DO,DF成等比數列,求![]()
![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com