Question

已知c=3，
（I）A={1，2，3，4，5}，在集合A中任取元素分別作為a，b的值（a，b的值可以相等，也可以不相等），求以a，b，c為三邊長且能構成三角形的概率；
（II）B=[1，5]，在區間B中任取元素分別作為a，b的值（a，b的值可以相等也可以不相等），求以a，b，c為三邊長且能構成三角形的概率．

Answer 1

分析：（Ⅰ）把（a，b）看成一個基本事件，則基本事件總數有25個，滿足條件|a-b|≥3或a+b≤3的基本事件有9個，這9個都不能構成三角形，最后利用對立事件得到能構成三角形的概率．
（Ⅱ）a，b，c能構成三角形的充要條件是

1＜a＜5 1＜b＜5 |a-b＜3 a+b＞3

，在坐標系aob內畫出滿足以上條件的區域，如圖所示，根據幾何概型的計算方法即可求得結果．

解答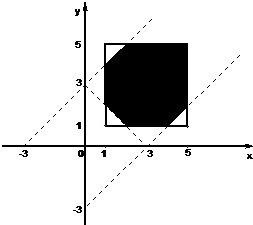：解：（Ⅰ）把（a，b）看成一個基本事件，則基本事件總數有25個，滿足條件|a-b|≥3或a+b≤3的基本事件有9個，這9個都不能構成三角形，所以能構成三角形的概率為P=1-

9

25

=

16

25

．…（5分）
（Ⅱ）以a，b，c為三邊長，能構成三角形
則a，b滿足關系：

1＜a＜5 1＜b＜5 |a-b＜3 a+b＞3

，它表示的平面區域如圖所示，…（8分）
所以，所球的概率為：P=1-

1.5

16

=

29

32

．…（10分）

點評：本題考查古典概型和幾何概型的概率估算公式中的“幾何度量”，可以為線段長度、面積、體積等，而且這個“幾何度量”只與“大小”有關，而與形狀和位置無關．解決的步驟均為：求出滿足條件A的基本事件對應的“幾何度量”N（A），再求出總的基本事件對應的“幾何度量”N，最后根據P=

N(A)

N

求解．屬中檔題．