
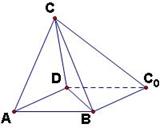
如圖,一張平行四邊形的硬紙片![]() 中,
中,![]() ,
,![]() 。沿它的對角線
。沿它的對角線![]() 把△
把△![]() 折起,使點
折起,使點![]() 到達平面
到達平面![]() 外點
外點![]() 的位置。
的位置。
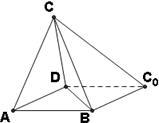
(Ⅰ)證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)如果△![]() 為等腰三角形,求二面角
為等腰三角形,求二面角![]() 的大小。
的大小。
解:(Ⅰ)證明:因為![]()
![]() ,
,![]() ,
,
所以![]() ,
,![]() 。
。
因為折疊過程中,![]() ,
,
所以![]() ,又
,又![]() ,故
,故![]() 平面
平面![]() 。
。
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() 。
。
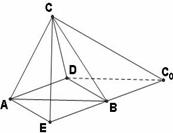
(Ⅱ)解法一:如圖,延長![]() 到
到![]() ,使
,使![]() ,連結
,連結![]() ,
,![]() 。
。
因為![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() 為正方形,
為正方形,![]() 。
。
由于![]() ,
,![]() 都與平面
都與平面![]() 垂直,所以
垂直,所以![]() ,可知
,可知![]() 。
。
因此只有![]() 時,△
時,△![]() 為等腰三角形。
為等腰三角形。
在![]() △
△![]() 中,
中,![]() ,又
,又![]() ,
,
所以△![]() 為等邊三角形,
為等邊三角形,![]() 。
。
由(Ⅰ)可知,,所以![]() 為二面角
為二面角![]() 的平面角,即二面角
的平面角,即二面角![]() 的大小為
的大小為![]() 。
。
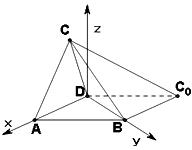
解法二:以![]() 為坐標原點,射線
為坐標原點,射線![]() ,
,![]() 分別為
分別為![]() 軸正半軸和
軸正半軸和![]() 軸正半軸,建立如圖的空間直角坐標系
軸正半軸,建立如圖的空間直角坐標系![]() ,則
,則![]() ,
,![]() ,
,![]() 。
。
由(Ⅰ)可設點![]() 的坐標為
的坐標為![]() ,其中
,其中![]() ,則有
,則有![]() 。 ①
。 ①
因為△![]() 為等腰三角形,所以
為等腰三角形,所以![]() 或
或![]() 。
。
若![]() ,則有
,則有![]() 。
。
則此得![]() ,
,![]() ,不合題意。
,不合題意。
若![]() ,則有
,則有![]() 。 ②
。 ②
聯立①和②得![]() ,
,![]() 。故點
。故點![]() 的坐標為
的坐標為![]() 。
。
由于![]() ,
,![]() ,所以
,所以![]() 與
與![]() 夾角的大小等于二面角
夾角的大小等于二面角![]() 的大小。
的大小。
又![]() ,
,![]() ,
,![]()
所以![]() 即二面角
即二面角![]() 的大小為
的大小為![]() 。
。


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
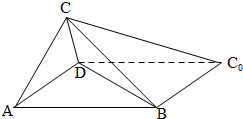 如圖,一張平行四邊形的硬紙片ABC0D中,AD=BD=1,AB=
如圖,一張平行四邊形的硬紙片ABC0D中,AD=BD=1,AB=| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
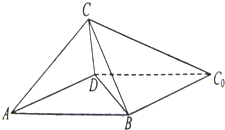 如圖,一張平行四邊形的硬紙片ABC0D中,AD=BD=1,AB=
如圖,一張平行四邊形的硬紙片ABC0D中,AD=BD=1,AB=| 2 |
查看答案和解析>>
科目:高中數學 來源:2012屆度湖南省高三下學期二輪復習理科數學試卷 題型:解答題
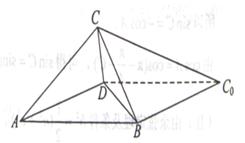
如圖,一張平行四邊形的硬紙片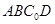 中,
中,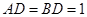 ,
, 。沿它的對角線
。沿它的對角線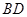 把△
把△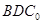 折起,使點
折起,使點 到達平面
到達平面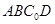 外點
外點 的位置。
的位置。
(Ⅰ)△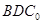 折起的過程中,判斷平面
折起的過程中,判斷平面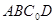 與平面
與平面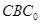 的位置關系,并給出證明;
的位置關系,并給出證明;
(Ⅱ)當△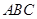 為等腰三角形,求此時二面角
為等腰三角形,求此時二面角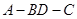 的大小。
的大小。
查看答案和解析>>
科目:高中數學 來源:河北省2009-2010學年度第二學期二調考試高一年級數學試卷理科 題型:解答題
(本小題共12分)如圖,一張平行四邊形的硬紙片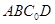 中,
中,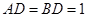 ,
,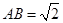 。沿它的對角線
。沿它的對角線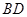 把△
把△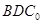 折起,使點
折起,使點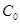 到達平面
到達平面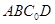 外點
外點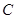 的位置。
的位置。
(Ⅰ)證明:平面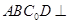 平面
平面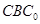 ;
;
(Ⅱ)如果△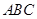 為等腰三角形,求二面角
為等腰三角形,求二面角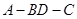 的大小。
的大小。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com