
【題目】為提高市場銷售業績,某公司設計兩套產品促銷方案(方案1運作費用為![]() 元/件;方案2的的運作費用為
元/件;方案2的的運作費用為![]() 元/件),并在某地區部分營銷網點進行試點(每個試點網點只采用一種促銷方案),運作一年后,對比該地區上一年度的銷售情況,分別統計相應營銷網點個數,制作相應的列聯表如下表所示.
元/件),并在某地區部分營銷網點進行試點(每個試點網點只采用一種促銷方案),運作一年后,對比該地區上一年度的銷售情況,分別統計相應營銷網點個數,制作相應的列聯表如下表所示.
無促銷活動 | 采用促銷方案1 | 采用促銷方案2 | ||
本年度平均銷售額不高于上一年度平均銷售額 | 48 | 11 | 31 | 90 |
本年度平均銷售額高于上一年度平均銷售額 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)請根據列聯表提供的信息,為該公司今年選擇一套較為有利的促銷方案(不必說明理由);
(Ⅱ)已知該公司產品的成本為10元/件(未包括促銷活動運作費用),為制定本年度該地區的產品銷售價格,統計上一年度的![]() 組售價
組售價![]() (單位:元/件,整數)和銷量
(單位:元/件,整數)和銷量![]() (單位:件)(
(單位:件)(![]() )如下表所示:
)如下表所示:
售價 |
|
|
|
|
|
|
|
|
銷量 |
|
|
|
|
|
|
|
|
(ⅰ)請根據下列數據計算相應的相關指數![]() ,并根據計算結果,選擇合適的回歸模型進行擬合;
,并根據計算結果,選擇合適的回歸模型進行擬合;
(ⅱ)根據所選回歸模型,分析售價![]() 定為多少時?利潤
定為多少時?利潤![]() 可以達到最大.
可以達到最大.
|
|
| |
|
|
|
|
|
| ||
參考公式:相關指數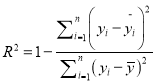 .
.
【答案】(Ⅰ)見解析;(Ⅱ)(ⅰ)![]() 進行擬合最為合適.(ⅱ)
進行擬合最為合適.(ⅱ) ![]() .
.
【解析】試題分析:(Ⅰ)由列聯表信息可知,年度平均銷售額與方案![]() 的運作相關性強于方案
的運作相關性強于方案![]() .
.
(Ⅱ)(ⅰ)由已知數據可知,經過計算可得![]() ,即可選擇采用回歸模型
,即可選擇采用回歸模型![]() 進行擬合最為合適.
進行擬合最為合適.
(ⅱ)由(Ⅰ)可知,采用方案![]() 的運作效果較方案
的運作效果較方案![]() 好,求得當售價
好,求得當售價![]() 時,利潤達到最大.
時,利潤達到最大.
試題解析:(Ⅰ)由列聯表信息可知,年度平均銷售額與方案![]() 的運作相關性強于方案
的運作相關性強于方案![]() .
.
(Ⅱ)(ⅰ)由已知數據可知,回歸模型![]() 對應的相關指數
對應的相關指數![]() ;
;
回歸模型![]() 對應的相關指數
對應的相關指數![]() ;
;
回歸模型![]() 對應的相關指數
對應的相關指數![]() .
.
因為![]() ,所以采用回歸模型
,所以采用回歸模型![]() 進行擬合最為合適.
進行擬合最為合適.
(ⅱ)由(Ⅰ)可知,采用方案![]() 的運作效果較方案
的運作效果較方案![]() 好,
好,
故年利潤![]() ,
, ![]() ,
,
當![]() 時,
時, ![]() 單調遞增;
單調遞增;
當![]() 時,
時, ![]() 單調遞減.
單調遞減.
故當售價![]() 時,利潤達到最大.
時,利潤達到最大.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知圓錐![]() 和圓柱
和圓柱![]() 的組合體(它們的底面重合),圓錐的底面圓
的組合體(它們的底面重合),圓錐的底面圓![]() 半徑為
半徑為![]() ,
, ![]() 為圓錐的母線,
為圓錐的母線, ![]() 為圓柱
為圓柱![]() 的母線,
的母線, ![]() 為下底面圓
為下底面圓![]() 上的兩點,且
上的兩點,且![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() 是圓
是圓![]() 上的任意一點,設
上的任意一點,設![]() 為該圓的圓心,并且線段
為該圓的圓心,并且線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 交于點
交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)已知![]() 兩點的坐標分別為
兩點的坐標分別為![]() ,
, ![]() ,點
,點![]() 是直線
是直線![]() 上的一個動點,且直線
上的一個動點,且直線![]() 分別交(1)中點
分別交(1)中點![]() 的軌跡于
的軌跡于![]() 兩點(
兩點(![]() 四點互不相同),證明:直線
四點互不相同),證明:直線![]() 恒過一定點,并求出該定點坐標.
恒過一定點,并求出該定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直角坐標系![]() 中,曲線
中,曲線![]() 與
與![]() 軸負半軸交于點
軸負半軸交于點![]() ,直線
,直線![]() 與
與![]() 相切于
相切于![]() ,
, ![]() 為
為![]() 上任意一點,
上任意一點, ![]() 為
為![]() 在
在![]() 上的射影,
上的射影, ![]() 為
為![]() 的中點.
的中點.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)軌跡![]() 與
與![]() 軸交于
軸交于![]() ,點
,點![]() 為曲線
為曲線![]() 上的點,且
上的點,且![]() ,
, ![]() ,試探究三角形
,試探究三角形![]() 的面積是否為定值,若為定值,求出該值;若非定值,求其取值范圍.
的面積是否為定值,若為定值,求出該值;若非定值,求其取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
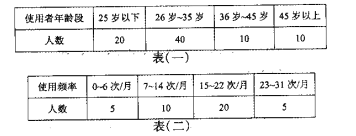
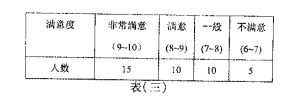
【題目】共享單車入住泉州一周年以來,因其“綠色出行,低碳環保”的理念而備受人們的喜愛,值此周年之際,某機構為了了解共享單車使用者的年齡段,使用頻率、滿意度等三個方面的信息,在全市范圍內發放![]() 份調查問卷,回收到有效問卷
份調查問卷,回收到有效問卷![]() 份,現從中隨機抽取
份,現從中隨機抽取![]() 份,分別對使用者的年齡段、
份,分別對使用者的年齡段、![]() ~
~![]() 歲使用者的使用頻率、
歲使用者的使用頻率、![]() ~
~![]() 歲使用者的滿意度進行匯總,得到如下三個表格:
歲使用者的滿意度進行匯總,得到如下三個表格:
(Ⅰ)依據上述表格完成下列三個統計圖形:
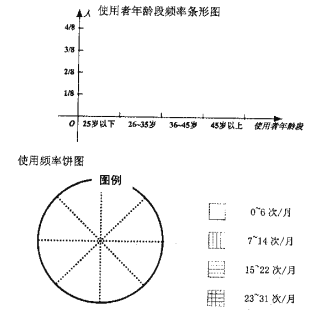
(Ⅱ)某城區現有常住人口![]() 萬,請用樣本估計總體的思想,試估計年齡在
萬,請用樣本估計總體的思想,試估計年齡在![]() 歲~
歲~![]() 歲之間,每月使用共享單車在
歲之間,每月使用共享單車在![]() ~
~![]() 次的人數.
次的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sin2x的圖象向左平移 ![]() 個單位,再向上平移1個單位,所得圖象的函數解析式是( )
個單位,再向上平移1個單位,所得圖象的函數解析式是( )
A.y=cos2x
B.y=2cos2x
C.![]()
D.y=2sin2x?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正三棱臺的上、下底面的邊長分別是3和6. 
(1)若側面與底面所成的角為60°,求此三棱臺的體積;
(2)若側棱與底面所成的角為60°,求此三棱臺的側面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com