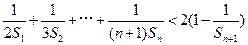某公司全年的利潤為
b元,其中一部分作為獎金發(fā)給
n位職工,獎金分配方案如下:首先將職工按工作業(yè)績(工作業(yè)績均不相同)從大到小,由1到
n排序,第1位職工得獎金
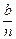
元,然后再將余額除以
n發(fā)給第2位職工,按此方法將獎金逐一發(fā)給每位職工,并將最后剩余部分作為公司發(fā)展基金.
(1)設
ak(1≤
k≤
n)為第
k位職工所得獎金金額,試求
a2,
a3,并用
k、
n和
b表示
ak(不必證明);
(2)證明
ak>
ak+1(
k=1,2,…,
n-1),并解釋此不等式關于分配原則的實際意義;
(3)發(fā)展基金與
n和
b有關,記為
Pn(
b),對常數(shù)
b,當
n變化時,求
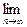 Pn
Pn(
b).
(1)
ak=

(1-

)
k-1b; (2) 獎金分配方案體現(xiàn)了“按勞分配”或“不吃大鍋飯”的原則;(3)

.
(1)第1位職工的獎金
a1=

,
第2位職工的獎金
a2=

(1-

)
b,
第3位職工的獎金
a3=

(1-

)
2b,…,
第
k位職工的獎金
ak=

(1-

)
k-1b;
(2)
ak-
ak+1=

(1-

)
k-1b>0,此獎金分配方案體現(xiàn)了“按勞分配”或“不吃大鍋飯”的原則。
(3)設
fk(
b)表示獎金發(fā)給第
k位職工后所剩余數(shù),
則
f1(
b)=(1-

)
b,
f2(
b)=(1-

)
2b,…,
fk(
b)=(1-

)
kb.
得
Pn(
b)=
fn(
b)=(1-

)
nb,
故

.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
f(
x)=
a1x+
a2x2+
a3x3+…+
anxn,
n∈N
*且
a1、
a2、
a3、……、
an構成一個數(shù)列{
an},滿足
f(1)=
n2.
(1)求數(shù)列{
an}的通項公式,并求
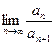
;
(2)證明0<
f(

)<1.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)設數(shù)列
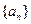
的前
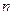
和為
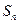
,已知
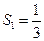
,
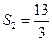
,
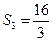
,
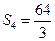
,
一般地,
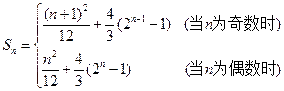
(
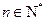
).
(Ⅰ)求
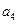
;(Ⅱ)求
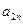
;(Ⅲ)求和:
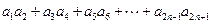
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列{
an}為等差數(shù)列,公差
d≠0,由{
an}中的部分項組成的數(shù)列
a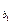
,
a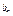
,…,
a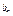
,…為等比數(shù)列,其中
b1=1,
b2=5,
b3=17.
(1)求數(shù)列{
bn}的通項公式;
(2)記
Tn=C
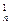 b1
b1+C
 b2
b2+C
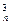 b3
b3+…+C
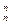 bn
bn,求
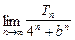
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(12分)已知
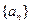
是各項都為正數(shù)的數(shù)列,
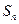
為其前
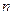
項的和,且
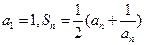
(I)分別求
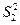
,
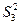
的值;(II)求數(shù)列
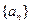
的通項
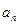
;(III)求證:
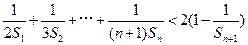
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在等差數(shù)列
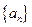
中,已知
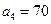
,
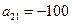
.
(1)求首項
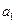
與公差
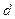
,并寫出通項公式;
(2)
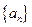
中有多少項屬于區(qū)間
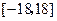
?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設
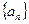
是首項為1的正項數(shù)列,且
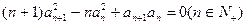
,
則數(shù)列
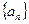
的通項
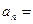
.
查看答案和解析>>

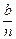 元,然后再將余額除以n發(fā)給第2位職工,按此方法將獎金逐一發(fā)給每位職工,并將最后剩余部分作為公司發(fā)展基金.
元,然后再將余額除以n發(fā)給第2位職工,按此方法將獎金逐一發(fā)給每位職工,并將最后剩余部分作為公司發(fā)展基金.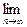 Pn(b).
Pn(b).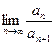 ;
; )<1.
)<1.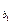 ,a
,a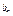 ,…,a
,…,a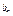 ,…為等比數(shù)列,其中b1=1,b2=5,b3=17.
,…為等比數(shù)列,其中b1=1,b2=5,b3=17.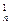 b1+C
b1+C b2+C
b2+C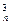 b3+…+C
b3+…+C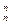 bn,求
bn,求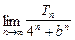 .
.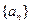 是各項都為正數(shù)的數(shù)列,
是各項都為正數(shù)的數(shù)列,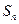 為其前
為其前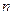 項的和,且
項的和,且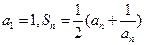
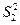 ,
,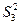 的值;(II)求數(shù)列
的值;(II)求數(shù)列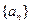 的通項
的通項 ;(III)求證:
;(III)求證: