
【題目】已知拋物線y2=2px(p>0)上一點P(3,t)到其焦點的距離為4.
(1)求p的值;
(2)過點Q(1,0)作兩條直線l1 , l2與拋物線分別交于點A、B和C、D,點M,N分別是線段AB和CD的中點,設直線l1 , l2的斜率分別為k1 , k2 , 若k1+k2=3,求證:直線MN過定點.
【答案】解:(1)拋物線y2=2px的焦點為(![]() ,0),準線為x=﹣
,0),準線為x=﹣![]() ,
,
由拋物線的定義可得,3+![]() =4,解得p=2;
=4,解得p=2;
(2)證明:由題意知,k1+k2=3,
不妨設AB的斜率k1=k,則CD的斜率k2=3﹣k,
所以AB的直線方程是:y=k(x﹣1),CD的直線方程是y=(3﹣k)(x﹣1),
設A(x1 , y1),B(x2 , y2),
由 ![]() ,得,k2x2﹣(2k2+4)x+k2=0,
,得,k2x2﹣(2k2+4)x+k2=0,
則x1+x2=![]() ,x1x2=1,
,x1x2=1,
所以y1+y2=k(x1﹣1)+k(x2﹣1)=k(2+![]() )﹣2k=
)﹣2k=![]() ,
,
因為M是AB的中點,所以點M(1+![]() ,
,![]() ),
),
同理可得,點N(1+![]() ,
,![]() ),
),
所以直線MN的方程是:y﹣![]() =
=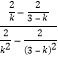 (x﹣1﹣
(x﹣1﹣![]() ),
),
化簡得,y=(k﹣k2)(x﹣1)+![]() ,令x=1,得y=
,令x=1,得y=![]() ,
,
所以直線MN過定點(1,![]() ).
).
【解析】(1)求得拋物線的焦點和準線方程,運用拋物線的定義,可得p=2;
(2)不妨設AB的斜率k1=k,求出CD的斜率k2=3﹣k,利用點斜式方程求出直線AB、CD的方程,與拋物線方程聯立消x得關于y的一元二次方程,根據韋達定理即可求得中點M、N的坐標,利用點斜式方程求出直線MN的方程,化簡后求出直線MN經過的定點坐標.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:
【題目】在獨立性檢驗中,統計量![]() 有三個臨界值:2.706,3.841和6.635.當
有三個臨界值:2.706,3.841和6.635.當![]() 時,有90%的把握說明兩個事件有關;當
時,有90%的把握說明兩個事件有關;當![]() 時,有95%的把握說明兩個事件有關,當
時,有95%的把握說明兩個事件有關,當![]() 時,有99%的把握說明兩個事件有關,當
時,有99%的把握說明兩個事件有關,當![]() 時,認為兩個事件無關.在一項打鼾與心臟病的調查中,共調查了2000人,經計算
時,認為兩個事件無關.在一項打鼾與心臟病的調查中,共調查了2000人,經計算![]() .根據這一數據分析,認為打鼾與患心臟病之間( )
.根據這一數據分析,認為打鼾與患心臟病之間( )
A. 有95%的把握認為兩者有關 B. 約95%的打鼾者患心臟病
C. 有99%的把握認為兩者有關 D. 約99%的打鼾者患心臟病
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+![]() , g(x)=x+lnx,其中a>0,且x∈(0,+∞).
, g(x)=x+lnx,其中a>0,且x∈(0,+∞).
(1)若a=1,求f(x)的最小值;
(2)若對任意x≥1,不等式f(x)≤g(x)恒成立,求實數a的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱柱ABCD-A1B1C1D1中,![]() ,平面BB1C1C
,平面BB1C1C![]() 底面ABCD,點
底面ABCD,點![]() 、F分別是線段
、F分別是線段![]() 、BC的中點.
、BC的中點.
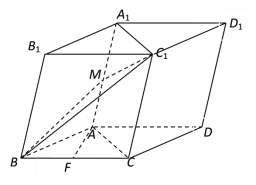
(1)求證:AF//平面![]() ;
;
(2)求證:平面BB1C1C⊥平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題:①在線性回歸模型中,相關指數![]() 表示解釋變量
表示解釋變量![]() 對于預報變量
對于預報變量![]() 的貢獻率,
的貢獻率, ![]() 越接近于1,表示回歸效果越好;②兩個變量相關性越強,則相關系數的絕對值就越接近于1;③在回歸直線方程
越接近于1,表示回歸效果越好;②兩個變量相關性越強,則相關系數的絕對值就越接近于1;③在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均減少0.5個單位;④對分類變量
平均減少0.5個單位;④對分類變量![]() 與
與![]() ,它們的隨機變量
,它們的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說, ![]() 越小,“
越小,“![]() 與
與![]() 有關系”的把握程度越大.其中正確命題的個數是( )
有關系”的把握程度越大.其中正確命題的個數是( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年10月19日,由中國工信部、江西省政府聯合主辦的世界VR(虛擬現實)產業大會在南昌開幕,南昌在紅谷灘新區建立VR特色小鎮項目.現某廠商抓住商機在去年用450萬元購進一批VR設備,經調試后今年投入使用,計劃第一年維修、保養費用22萬元,從第二年開始,每年所需維修、保養費用比上一年增加4萬元,該設備使用后,每年的總收入為180萬元,設使用x年后設備的盈利額為y萬元.
(1)寫出y與x之間的函數關系式;
(2)使用若干年后,當年平均盈利額達到最大值時,求該廠商的盈利額.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉軸旋轉,有下列結論:
①當直線AB與a成60°角時,AB與b成30°角;
②當直線AB與a成60°角時,AB與b成60°角;
③直線AB與a所成角的最小值為45°;
④直線AB與a所成角的最大值為60°.
其中正確的是________.(填寫所有正確結論的編號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com