
【題目】某公司在迎新年晚會上舉行抽獎活動,有甲、乙兩個抽獎方案供員工選擇;
方案甲:員工最多有兩次抽獎機會,每次抽獎的中獎率為 ![]() .第一次抽獎,若未中獎,則抽獎結束.若中獎,則通過拋一枚質地均勻的硬幣,決定是否繼續進行第二次抽獎,規定:若拋出硬幣,反面朝上,員工則獲得500元獎金,不進行第二次抽獎;若正面朝上,員工則須進行第二次抽獎,且在第二次抽獎中,若中獎,獲得獎金1000元;若未中獎,則所獲獎金為0元.
.第一次抽獎,若未中獎,則抽獎結束.若中獎,則通過拋一枚質地均勻的硬幣,決定是否繼續進行第二次抽獎,規定:若拋出硬幣,反面朝上,員工則獲得500元獎金,不進行第二次抽獎;若正面朝上,員工則須進行第二次抽獎,且在第二次抽獎中,若中獎,獲得獎金1000元;若未中獎,則所獲獎金為0元.
方案乙:員工連續三次抽獎,每次中獎率均為 ![]() ,每次中獎均可獲獎金400元.
,每次中獎均可獲獎金400元.
(1)求某員工選擇方案甲進行抽獎所獲獎金 ![]() (元)的分布列;
(元)的分布列;
(2)某員工選擇方案乙與選擇方案甲進行抽獎,試比較哪個方案更劃算?
【答案】
(1)解:(1) ![]() ,
, ![]() ,
,
![]() .
.
所以某員工選擇方案甲進行抽獎所獲金 ![]() (元)的分布列為:
(元)的分布列為:
|
| 500 | 1000 |
|
|
|
|
(2)解:由(1)可知,選擇方案甲進行抽獎所獲得獎金 ![]() 的均值
的均值 ![]() ,
,
若選擇方案乙進行抽獎中獎次數 ![]() ,則
,則 ![]() ,
,
抽獎所獲獎金 ![]() 的均值
的均值 ![]() ,故答案為:擇方案甲較劃算.
,故答案為:擇方案甲較劃算.
【解析】(1)根據題意先求出X的取值,再利用概率的定義分別求出各個值下的概率列表即可。(2)由題意比較方案甲和方案乙進行抽獎所獲獎金X的均值,即可得到選擇更大的一種方案。
【考點精析】解答此題的關鍵在于理解離散型隨機變量及其分布列的相關知識,掌握在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


科目:高中數學 來源: 題型:
【題目】已知直線l過定點P(1,1),且傾斜角為 ![]() ,以坐標原點為極點,x軸的正半軸為極軸的坐標系中,曲線C的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸的坐標系中,曲線C的極坐標方程為 ![]() .
.
(1)求曲線C的直角坐標方程與直線l的參數方程;
(2)若直線l與曲線C相交于不同的兩點A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的個數為( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分條件;
③命題“若m≤ ![]() ,則方程mx2+2x+2=0有實數根”的否命題為真命題.
,則方程mx2+2x+2=0有實數根”的否命題為真命題.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠對新研發的一種產品進行試銷,得到如下數據表:
(1)根據上表求出回歸直線方程 ![]() ,并預測當單價定為8.3元時的銷量;
,并預測當單價定為8.3元時的銷量;
(2)如果該工廠每件產品的成本為5.5元,利用所求的回歸方程,要使得利潤最大,單價應該定為多少?
附:線性回歸方程 ![]() 中斜率和截距最小二乘估計計算公式:
中斜率和截距最小二乘估計計算公式: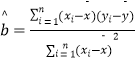 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C1的圓心在坐標原點O,且恰好與直線![]() 相切.
相切.
(Ⅰ)求圓C1的標準方程;
(Ⅱ)設點A為圓上一動點,AN垂直于x軸于點N,若動點Q滿足![]()
(其中m為非零常數),試求動點Q的軌跡方程;
(Ⅲ)在(Ⅱ)的結論下,當m=![]() 時,得到動點Q的軌跡為曲線C,與l1垂直的直線l與曲線C交于B,D兩點,求△OBD面積的最大值.
時,得到動點Q的軌跡為曲線C,與l1垂直的直線l與曲線C交于B,D兩點,求△OBD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,已知
,已知![]() ,其中
,其中![]() 為原點,
為原點,![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() ,求直線的
,求直線的![]() 斜率的取值范圍.
斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:①若 ![]() ,則
,則 ![]() 或
或 ![]() ;
;
② ![]() ,都有
,都有 ![]() ;
;
③若 ![]() 是實數,則
是實數,則 ![]() 是
是 ![]() 的充分不必要條件;
的充分不必要條件;
④“ ![]() ” 的否定是“
” 的否定是“ ![]() ” ;
” ;
其中真命題的個數是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高級中學今年高一年級招收“國際班”學生![]() 人,學校為這些學生開辟了直升海外一流大學的綠色通道,為了逐步提高這些學生與國際教育接軌的能力,將這
人,學校為這些學生開辟了直升海外一流大學的綠色通道,為了逐步提高這些學生與國際教育接軌的能力,將這![]() 人分為三個批次參加國際教育研修培訓,在這三個批次的學生中男、女學生人數如下表:
人分為三個批次參加國際教育研修培訓,在這三個批次的學生中男、女學生人數如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名,抽到第一批次、第二批次中女學生的概率分別是
名,抽到第一批次、第二批次中女學生的概率分別是![]() .
.
(1)求![]() 的值;
的值;
(2)為了檢驗研修的效果,現從三個批次中按分層抽樣的方法抽取![]() 名同學問卷調查,則三個批次被選取的人數分別是多少?
名同學問卷調查,則三個批次被選取的人數分別是多少?
(3)若從第(2)小問選取的學生中隨機選出兩名學生進行訪談,求“參加訪談的兩名同學至少有一個人來自第一批次”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com