
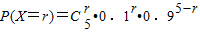 ,r=0,1,2,3,4,5,分別可得概率值,進而可得分布列,可得期望;
,r=0,1,2,3,4,5,分別可得概率值,進而可得分布列,可得期望; ,分別代入可得f的值,比較可得最小值,進而可得對應的n值.
,分別代入可得f的值,比較可得最小值,進而可得對應的n值.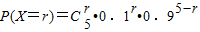 ,r=0,1,2,3,4,5,…(2分)
,r=0,1,2,3,4,5,…(2分)| X | 1 | 2 | 3 | 4 | 5 | |
| P | 0.59 | 0.33 | 0.073 | 0.0081 | 0.00045 | 0.00001 |
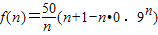 =
=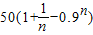 ,…(8分)
,…(8分)

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2013屆海南省高二下學期期末考試理科數學試卷(解析版) 題型:解答題
下表是某地區的一種傳染病與飲用水的調查表:
|
|
得病 |
不得病 |
合計 |
|
干凈水 |
52 |
466 |
518 |
|
不干凈水 |
94 |
218 |
312 |
|
合計 |
146 |
684 |
830 |
利用列聯表的獨立性檢驗,判斷能否以99.9%的把握認為“該地區的傳染病與飲用不干凈的水有關”
參考數據:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com