
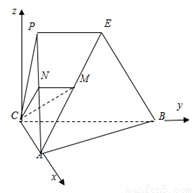
(本題滿分14分)如圖,平面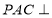 平面
平面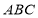 ,
, ,
,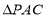 為等邊三角形,
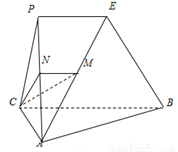
為等邊三角形,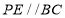 ,過
,過 作平面交
作平面交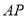 、
、 分別于點
分別于點 、
、 .
.
(1)求證: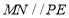 ;
;
(2) 設 ,求
,求 的值,使得平面
的值,使得平面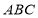 與平面
與平面 所成的銳二面角的大小為
所成的銳二面角的大小為 .
.
(1)詳見解析;(2)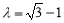 .
.
【解析】
試題分析:(1)根據條件中給出的平面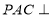 平面
平面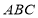 ,
,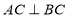 ,因此可以考慮以點
,因此可以考慮以點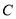 為原點建立空間直角坐標系,利用空間向量來求證,從而只需求出平面
為原點建立空間直角坐標系,利用空間向量來求證,從而只需求出平面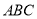 的一個法向量
的一個法向量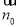 ,說明
,說明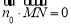 ,即有
,即有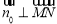 ,從而有
,從而有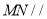 平面
平面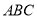 ,進而有
,進而有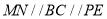 ;(2)由(1)建立的空間直角坐標系可知,問題等價于求得平面
;(2)由(1)建立的空間直角坐標系可知,問題等價于求得平面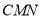 的一個法向量
的一個法向量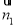 ,滿足
,滿足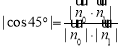 ,通過空間向量的計算,易知可取
,通過空間向量的計算,易知可取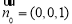 ,
,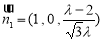 ,從而解得
,從而解得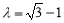 .
.
試題解析:(1)如圖以點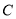 為原點建立空間直角坐標系
為原點建立空間直角坐標系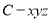 ,不妨設
,不妨設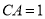 ,
,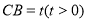 ,
,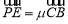 ,則
,則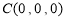 ,
, 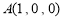 ,
,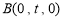 ,
,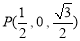 ,
, ,由
,由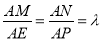 ,得
,得
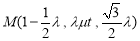 ,
,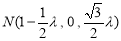 ,
,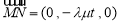 ,
,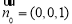 是平面
是平面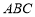 的一個法向量,且
的一個法向量,且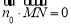 ,故
,故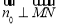 ,又∵
,又∵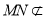 平面
平面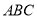 ,即知
,即知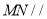 平面
平面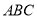 ,又∵
,又∵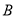 ,
,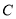 ,
,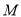 ,
,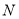 四點共面,∴
四點共面,∴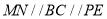 ;(2)
;(2) ,
,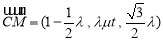 ,設平面
,設平面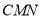 的法向量
的法向量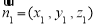 ,則
,則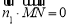 ,
,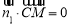 ,可取
,可取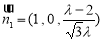 ,又∵
,又∵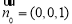 是平面
是平面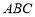 的一個法向量,由
的一個法向量,由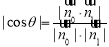 ,以及
,以及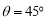 可得
可得 ,即
,即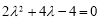 ,解得
,解得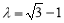 (負值舍去),故
(負值舍去),故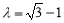 .
.
考點:立體幾何中的空間向量方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2015屆浙江省高三上學期期中考試文科數學試卷(解析版) 題型:選擇題
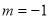 是直線
是直線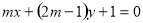 和直線
和直線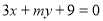 垂直的( )
垂直的( )
A.充分不必要條件 B.必要不充分條件
C.充分必要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省溫州市十校聯合體高三上學期期中聯考文科數學試卷(解析版) 題型:選擇題
已知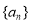 是等差數列,其前
是等差數列,其前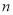 項和為
項和為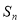 ,若
,若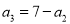 ,則
,則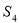 =( )
=( )
A.15 B.14 C.13 D.12
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省等四校高三上學期期中聯考理科數學試卷(解析版) 題型:選擇題
已知函數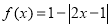 ,
,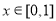 .定義:
.定義: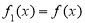 ,
,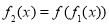 ,……,
,……,
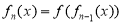 ,
,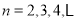 滿足
滿足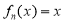 的點
的點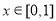 稱為
稱為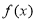 的
的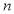 階不動點.則
階不動點.則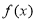 的
的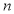 階不動點的個數是( )
階不動點的個數是( )
A.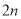 個 B.
個 B. 個 C.
個 C.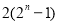 個 D.
個 D.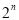 個
個
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省等四校高三上學期期中聯考理科數學試卷(解析版) 題型:選擇題
設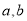 為實數,命題甲:
為實數,命題甲: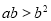 ,命題乙:
,命題乙: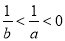 ,則甲是乙的( )
,則甲是乙的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2015屆浙江省富陽市高二下學期期中考試理科數學試卷(解析版) 題型:填空題
已知定義在R上的奇函數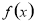 滿足
滿足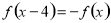 ,且在區間[0,2]上是增函數,若方程
,且在區間[0,2]上是增函數,若方程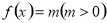 ,在區間[-8,8]上有四個不同的根
,在區間[-8,8]上有四個不同的根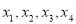 ,則
,則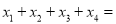 ______.
______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com