已知數(shù)列{a
n}的前n項和為S
n,對一切正整數(shù)n,點P
n(n,S
n)都在函數(shù)f(x)=x
2+2x的圖象上.
(1)求數(shù)列{a
n}的通項公式;
(2)設(shè)c
n=t
an(t>0),數(shù)列{c
n}的前n項和T
n,求
的值.
考點:數(shù)列的求和
專題:等差數(shù)列與等比數(shù)列
分析:(1)由于點P
n(n,S
n)都在函數(shù)f(x)=x
2+2x的圖象上.可得
Sn=n2+2n,當n≥2時,a
n=S
n-S
n-1=2n+1,當n=1時,a
1=S
1,即可得出.
(2)c
n=t
an=t
2n+1,可得當t=1時,數(shù)列{c
n}的前n項和T
n=n,
=
=1.當t>0且t≠1時,數(shù)列{c
n}的前n項和T
n=
,
=
.對t分為t>1與0<t<1即可得出.
解答:
解:(1)∵點P
n(n,S
n)都在函數(shù)f(x)=x
2+2x的圖象上.
∴
Sn=n2+2n,
當n≥2時,a
n=S
n-S
n-1=n
2+2n-[(n-1)
2+2(n-1)]=2n+1,
當n=1時,a
1=S
1=3,上式也成立.
∴a
n=2n+1.
(2)c
n=t
an=t
2n+1,
∴當t=1時,數(shù)列{c
n}的前n項和T
n=n,
=
=1.
當t>0且t≠1時,數(shù)列{c
n}的前n項和T
n=
,
∴
=
.
當t>1時,
=
=
=t
2.
當0<t<1時,
=
=1.
綜上可得:
=
.
點評:本題考查了遞推式的應(yīng)用、等比數(shù)列的前n項和公式、數(shù)列極限的運算性質(zhì),考查了分類討論的思想方法,考查了推理能力與計算能力,屬于難題.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
復(fù)數(shù)
在復(fù)平面內(nèi)對應(yīng)的點位于第
象限.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
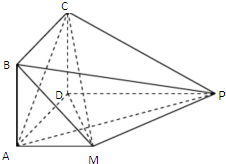
如圖,四邊形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
PD=2.
(1)求證:平面ABCD⊥平面AMPD;
(2)求點A到面CMP的距離.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知橢圓
+
=1上一點P與橢圓的兩個焦點F
1、F
2的連線互相垂直.
(1)求離心率和準線方程;
(2)求△PF
1F
2的面積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
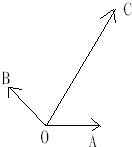
如圖,|
|=|
|=1,∠AOB=150°,∠AOC=60°,|
|=5.
(1)試用
、
表示
;
(2)求
•
的值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在△ABC中,a,b,c分別為三個內(nèi)角A,B,C的對邊,且acosB=3,bsinA=4.
(1)求邊長a;
(2)若△ABC的面積S=10,求△ABC的周長.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
數(shù)列{an}滿足:an+1=an+2(n∈N*)且a4=9.
(Ⅰ)求數(shù)列{an}的通項公式;
(Ⅱ)公比為q的等比數(shù)列{bn}滿足:b1=a2-1,q2-(a3+1)q+16=0,求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知f(x)=
sinωx-2sin
2(ω>0)的最小正周期為π.
(Ⅰ)當x∈[
,
]時,求函數(shù)f(x)的最小值;
(Ⅱ)在△ABC中,若f(C)=1,且2sin
2A=sinB+sin(A-C),求角A,B的值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
定義在R上的函數(shù)滿足f(x)=f(x+2),當x∈[1,3]時,f(x)=2-|x-2|,則( )
| A、f(sin)<f(cos) |
| B、f (sin1)>f (cos1) |
| C、f(cos)<f(sin) |
| D、f (cos2)>f (sin2) |
查看答案和解析>>



 如圖,四邊形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如圖,四邊形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD= 如圖,|
如圖,|