
【題目】某公司生產一批![]() 產品需要原材料500噸,每噸原材料可創造利潤12萬元,該公司通過設備升級,生產這批
產品需要原材料500噸,每噸原材料可創造利潤12萬元,該公司通過設備升級,生產這批![]() 產品所需原材料減少了
產品所需原材料減少了![]() 噸,且每噸原材料創造的利潤提高了
噸,且每噸原材料創造的利潤提高了![]() ;若將少用的
;若將少用的![]() 噸原材料全部用于生產公司新開發的
噸原材料全部用于生產公司新開發的![]() 產品,每噸原材料創造的利潤為
產品,每噸原材料創造的利潤為![]() 萬元,其中
萬元,其中![]() .
.
(1)若設備升級后生產這批![]() 產品的利潤不低于原來生產該批
產品的利潤不低于原來生產該批![]() 產品的利潤,求
產品的利潤,求![]() 的取值范圍;
的取值范圍;
(2)若生產這批![]() 產品的利潤始終不高于設備升級后生產這批
產品的利潤始終不高于設備升級后生產這批![]() 產品的利潤,求
產品的利潤,求![]() 的最大值.
的最大值.
 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
【題目】在長方體![]() 中,
中,![]() 分別是
分別是![]() 的中點,
的中點,![]() ,過
,過![]() 三點的的平面截去長方體的一個角后.得到如圖所示的幾何體
三點的的平面截去長方體的一個角后.得到如圖所示的幾何體![]() ,且這個幾何體的體積為
,且這個幾何體的體積為![]() .
.
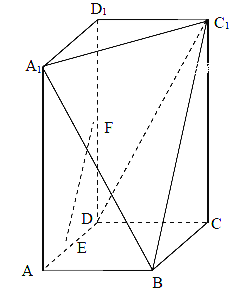
(1)求證:![]() 平面
平面![]() ;
;
(2)求![]() 的長;
的長;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使直線
,使直線![]() 與
與![]() 垂直,如果存在,求線段
垂直,如果存在,求線段![]() 的長,如果不存在,請說明理由.
的長,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上饒某中學研究性學習小組為調查市民喜歡觀看體育節目是否與性別有關,隨機抽取了55名市民,得數據如下表:
喜歡 | 不喜歡 | 合計 | |
男 | 20 | 5 | 25 |
女 | 10 | 20 | 30 |
合計 | 30 | 25 | 55 |
(1)判斷是否有99.5%的把握認為喜歡觀看體育節目與性別有關?
(2)用分層抽樣的方法從喜歡觀看體育節目的市民中隨機抽取6人作進一步調查,將這6位市民作為一個樣本,從中任選2人,求男市民人數![]() 的分布列和期望.
的分布列和期望.
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點
的中心在原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,右焦點到右頂點的距離為
,右焦點到右頂點的距離為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)是否存在與橢圓![]() 交于
交于![]() 兩點的直線
兩點的直線![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出實數
成立?若存在,求出實數![]() 的取值范圍,若不存在,請說明理由.
的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一批![]() 產品需要原材料500噸,每噸原材料可創造利潤12萬元,該公司通過設備升級,生產這批
產品需要原材料500噸,每噸原材料可創造利潤12萬元,該公司通過設備升級,生產這批![]() 產品所需原材料減少了
產品所需原材料減少了![]() 噸,且每噸原材料創造的利潤提高了
噸,且每噸原材料創造的利潤提高了![]() ;若將少用的
;若將少用的![]() 噸原材料全部用于生產公司新開發的
噸原材料全部用于生產公司新開發的![]() 產品,每噸原材料創造的利潤為
產品,每噸原材料創造的利潤為![]() 萬元,其中
萬元,其中![]() .
.
(1)若設備升級后生產這批![]() 產品的利潤不低于原來生產該批
產品的利潤不低于原來生產該批![]() 產品的利潤,求
產品的利潤,求![]() 的取值范圍;
的取值范圍;
(2)若生產這批![]() 產品的利潤始終不高于設備升級后生產這批
產品的利潤始終不高于設備升級后生產這批![]() 產品的利潤,求
產品的利潤,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從社會效益和經濟效益出發,某地投入資金進行生態環境建設,并以此發展旅游產業.根據規劃,本年度投入![]() 萬元,以后每年投入將比上年減少
萬元,以后每年投入將比上年減少![]() .本年度當地旅游業收入估計為
.本年度當地旅游業收入估計為![]() 萬元,由于該項建設對旅游業的促進作用,預計今后的旅游業收入每年會比上年增加
萬元,由于該項建設對旅游業的促進作用,預計今后的旅游業收入每年會比上年增加![]() .
.
(Ⅰ)設![]() 年內(本年度為第一年)總投入為
年內(本年度為第一年)總投入為![]() 萬元,旅游業總收入為
萬元,旅游業總收入為![]() 萬元.寫出
萬元.寫出![]() 的表達式;
的表達式;
(Ⅱ)至少經過幾年旅游業的總收入才能超過總投入?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的是_______(填序號)
①命題“![]() 有
有![]() ”的否定是“
”的否定是“![]() 有
有![]() ”;
”;
②若一個命題的逆命題為真命題,則它的否命題也一定為真命題;
③已知![]() ,
, ![]() ,若命題
,若命題![]() 為真命題,則
為真命題,則![]() 的取值范圍是
的取值范圍是![]() ;
;
④“![]() ”是“
”是“![]() ”成立的充分條件.
”成立的充分條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,直線
,直線![]() :
:![]() ,設圓
,設圓![]() 的半徑為1,圓心在
的半徑為1,圓心在![]() 上.
上.
(1)若圓心![]() 也在直線
也在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線,求切線方程;
的切線,求切線方程;
(2)若圓![]() 上存在點
上存在點![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com