【題目】已知
，現給出如下結論：
①
； ②
； ③
； ④
.
其中正確結論的序號為（ ）
A. ②③ B. ①④ C. ②④ D. ①③
【答案】A
【解析】分析：先求出f′（x），再進行因式分解，求出f′（x）＜0和f′（x）＞0對應x的范圍，即求出函數的單調區間和極值，再由條件判斷出a、b、c的具體范圍和f（1）＞0且f（2）＜0，進行求解得到abc的符號，進行判斷出f（0）的符號．
詳解：由題意得，f′（x）=3x2﹣9x+6=3（x﹣1）（x﹣2），
∴當x＜1或x＞2時，f′（x）＞0，當1＜x＜2時，f′（x）＜0，
∴函數f（x）的增區間是（﹣∞，1），（2，+∞），減區間是（1，2），
∴函數的極大值是f（1）=
，函數的極小值是f（2）=2﹣abc，
∵a＜b＜c，且f（a）=f（b）=f（c）=0，
∴a＜1＜b＜2＜c，f（1）＞0且f（2）＜0，解得2＜
，
∴f（0）=﹣abc＜0，
則f（0）f（1）＜0、f（0）f（2）＞0，
故答案為：A．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】對某種書籍的成本費
（元）與印刷冊數
（千冊）的數據作了初步處理，得到下面的散點圖及一些統計量的值.
表中
.
為了預測印刷20千冊時每冊的成本費，建立了兩個回歸模型：
.
（1）根據散點圖，擬認為選擇哪個模型預測更可靠?（只選出模型即可）
（2）根據所給數據和（1）中的模型選擇，求關于的回歸方程，并預測印刷20千冊時每冊的成本費.
附：對于一組數據
，其回歸方程
中斜率和截距的最小二乘估計公式分別為：
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某食品公司研發生產一種新的零售食品，從產品中抽取100件作為樣本，測量這些產品的一項質量指標值，由測量結果得到如下頻率分布直方圖：
(1)求直方圖中
的值；
(2)根據頻率分布直方圖估計樣本數據的眾數、中位數各是多少（結果保留整數）；
(3)由頻率分布直方圖可以認為，這種產品的質量指標值
服從正態分布
，試計算數據落在
上的概率.
（參考數據：若
，則
,
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解我市特色學校的發展狀況，某調查機構得到如下統計數據：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
特色學校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（Ⅰ）根據上表數據，計算
與
的相關系數
，并說明與的線性相關性強弱（已知：
，則認為與線性相關性很強；
，則認為與線性相關性一般；
，則認為與線性相關性較弱）；
（Ⅱ）求關于的線性回歸方程，并預測我市2019年特色學校的個數（精確到個）．
參考公式：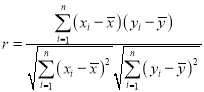 
，
，
，
，
，
．
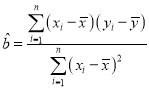查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓E： 
的焦點在x軸上
（1）若橢圓E的焦距為1，求橢圓E的方程；
（2）設F1 ， F2分別是橢圓E的左、右焦點，P為橢圓E上第一象限內的點，直線F2P交y軸于點Q，并且F1P⊥F1Q，證明：當a變化時，點P在某定直線上．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了評估A，B兩家快遞公司的服務質量，從兩家公司的客戶中各隨機抽取100名客戶作為樣本，進行服務質量滿意度調查，將A，B兩公司的調查得分分別繪制成頻率分布表和頻率分布直方圖．規定
分以下為對該公司服務質量不滿意．
分組 | 頻數 | 頻率 |
|
|
|
|
|
|
|
| 0.4 |
|
|
|
|
|
|
合計 |
|
|
（Ⅰ）求樣本中對B公司的服務質量不滿意的客戶人數；
（Ⅱ）現從樣本對A，B兩個公司服務質量不滿意的客戶中，隨機抽取2名進行走訪，求這兩名客戶都來自于B公司的概率；
（Ⅲ）根據樣本數據，試對兩個公司的服務質量進行評價，并闡述理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數，
），過點
的直線
的參數方程為
（
為參數）.
（Ⅰ）求曲線的普通方程，并說明它表示什么曲線；
（Ⅱ）設曲線與直線分別交于
，
兩點，若
，
，
成等比數列，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對某校高三年級學生參加社區服務次數進行統計，隨機抽取
名學生作為樣本，得到這名學生參加社區服務的次數．根據此數據作出了頻數與頻率的統計表和頻率分布直方圖：
分組 | 頻數 | 頻率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合計 |
| 1 |
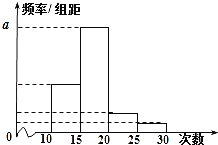
（1）求出表中，
及圖中
的值；
（2）若該校高三學生有240人，試估計該校高三學生參加社區服務的次數在區間
內的人數；
（3）在所取樣本中，從參加社區服務的次數不少于20次的學生中任選2人，求至多一人參加社區服務次數在區間
內的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
