
【題目】隨著快遞行業的崛起,中國快遞業務量驚人,2018年中國快遞量世界第一,已連續五年突破五百億件,完全超越美日歐的總和,穩居世界第一名.某快遞公司收取費的標準是:不超過1kg的包裹收費8元;超過1kg的包裹,在8元的基礎上,每超過1kg(不足1kg,按1kg計算)需再收4元.
該公司將最近承攬(接收并發送)的100件包裹的質量及件數統計如下(表1):
表1:

公司對近50天每天承攬包裹的件數(在表2中的“件數范圍”內取的一個近似數據)、件數范圍及天數,列表如下(表2):
表2:

(1)將頻率視為概率,計算該公司未來3天內恰有1天攬件數在100~299之間的概率;
(2)①根據表1中最近100件包裹的質量統計,估計該公司對承攬的每件包裹收取快遞費的平均值:
②根據以上統計數據,公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤,其余用作其他費用.目前,前臺有工作人員5人,每人每天攬件數不超過100件,日工資80元.公司正在考慮是否將前臺人員裁減1人,試計算裁員前、后公司每天攬件數的數學期望;若你是公司決策者,根據公司每天所獲利潤的期望值,決定是否裁減前臺工作人員1人?
【答案】(1)![]() (2) ①12 ②應裁減1人
(2) ①12 ②應裁減1人
【解析】
(1)根據獨立重復時間概率計算公式,可得未來3天內恰有1天攬件數在100~299之間的概率。
(2) ①求出收件費用與收件質量的函數關系式,再由平均數定義即可求得平均收件費用。
②根據收件數量與收件單價,可分別計算出裁減人員前后的利潤,比較即可判斷出是否需要裁減人員。
(1) 將頻率視為概率,計算該公司未來3天內恰有1天攬件數在100~299之間的概率為獨立重復事件
樣本中包裹件數在100~299之間的天數為![]() ,頻率為
,頻率為![]()
所以![]()
(2) ①設收件費用為y,收件質量為x,則
收件費用與收件質量的關系式為y=8+4(x-1)=4x+4
所以每件包裹收取快遞費的平均值為
![]()
②根據題意及①,攬件數每增加1,公司快遞收入增加12(元)
若不裁員,則每天可攬件的上限為500件,公司每日攬件數情況如下:
包裹件數范圍 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
實際攬件數(取中值) | 50 | 150 | 250 | 350 | 450 |
頻率 | 0.1 | 0.2 | 0.5 | 0.1 | 0.1 |
EY | 50×0.1+150×0.2+250×0.5+350×0.1+450×0.1=240 | ||||
所以公司每日利潤的期望值為![]() 元
元
若裁員1人,則每天可攬件的上限為400件,公司每日攬件數情況如下:
包裹件數范圍 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
實際攬件數(取中值) | 50 | 150 | 250 | 350 | 400 |
頻率 | 0.1 | 0.2 | 0.5 | 0.1 | 0.1 |
EY | 50×0.1+150×0.2+250×0.5+350×0.1+400×0.1=235 | ||||
所以公司每日利潤的期望值為![]() 元
元
因為560<620 ,所以公司應將前臺工作人員裁員1人。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知定點![]() ,動點
,動點![]() 異于原點
異于原點![]() 在y軸上運動,連接FP,過點P作PM交x軸于點M,并延長MP到點N,且
在y軸上運動,連接FP,過點P作PM交x軸于點M,并延長MP到點N,且![]() ,
,![]() .
.
![]() 求動點N的軌跡C的方程;
求動點N的軌跡C的方程;
![]() 若直線l與動點N的軌跡交于A、B兩點,若
若直線l與動點N的軌跡交于A、B兩點,若![]() 且
且![]() ,求直線l的斜率k的取值范圍.
,求直線l的斜率k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() 為參數),
為參數),![]() 是
是![]() 上的動點,且滿足
上的動點,且滿足![]() (
(![]() 為坐標原點),以原點
為坐標原點),以原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系,點
軸的正半軸為極軸建立極坐標系,點![]() 的極坐標為
的極坐標為![]()
(1)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的普通方程;
的普通方程;
(2)證明:![]() 為定值,并求
為定值,并求![]() 面積的最大值。
面積的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ADEF與梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M為CE的中點,N為CD中點.
,M為CE的中點,N為CD中點.
![]() 求證:平面
求證:平面![]() 平面ADEF;
平面ADEF;
![]() 求證:平面
求證:平面![]() 平面BDE;
平面BDE;
![]() 求點D到平面BEC的距離.
求點D到平面BEC的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在人群流量較大的街道,有一中年人吆喝“送錢”,只見他手拿一黑色小布袋,袋中有3只黃色、3只白色的乒乓球(其體積、質地完成相同),旁邊立著一塊小黑板寫道:
摸球方法:從袋中隨機摸出3個球,若摸得同一顏色的3個球,攤主送給摸球者5元錢;若摸得非同一顏色的3個球,摸球者付給攤主1元錢.
(1)摸出的3個球為白球的概率是多少?
(2)摸出的3個球為2個黃球1個白球的概率是多少?
(3)假定一天中有100人次摸獎,試從概率的角度估算一下這個攤主一個月(按30天計)能賺多少錢?
查看答案和解析>>
科目:高中數學 來源: 題型:
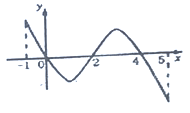
【題目】已知函數![]() 的定義域為
的定義域為![]() ,部分對應值如下表,
,部分對應值如下表,![]() 的導函數
的導函數![]() 的圖象如圖所示,給出關于
的圖象如圖所示,給出關于![]() 的下列命題:
的下列命題:
①函數![]() 在
在![]() 處取得極小值;
處取得極小值;
②函數![]() 在
在![]() 是減函數,在
是減函數,在![]() 是增函數;
是增函數;
③當![]() 時,函數
時,函數![]() 有4個零點;
有4個零點;
④如果當![]() 時,
時,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值為0.
的最小值為0.
其中所有的正確命題是__________(寫出正確命題的序號).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}為遞增的等差數列,數列{bn}滿足bn=anan+1an+2(n∈N*),設Sn為數列{bn}的前n項和,若a2![]() ,則當Sn取得最小值時n的值為( )
,則當Sn取得最小值時n的值為( )
A.14B.13C.12D.11
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com