
【題目】過點![]() 作拋物線
作拋物線![]() 的兩條切線, 切點分別為
的兩條切線, 切點分別為![]() ,
, ![]() .
.
(1) 證明: ![]() 為定值;
為定值;
(2) 記△![]() 的外接圓的圓心為點
的外接圓的圓心為點![]() , 點
, 點![]() 是拋物線
是拋物線![]() 的焦點, 對任意實數
的焦點, 對任意實數![]() , 試判斷以
, 試判斷以![]() 為直徑的圓是否恒過點
為直徑的圓是否恒過點![]() ? 并說明理由.
? 并說明理由.
【答案】(I)詳見解析;(II)詳見解析.
【解析】試題分析:(Ⅰ)對![]() 求導,得到直線
求導,得到直線![]() 的斜率為
的斜率為![]() ,進一步得到直線
,進一步得到直線![]() 的方程為
的方程為![]() . 將點點
. 將點點![]() 代入直線
代入直線![]() 方程,整理得
方程,整理得![]() .
.
同理, ![]() . 又
. 又![]() , 所以
, 所以![]() 為定值.
為定值.
(Ⅱ)由題意可得)直線![]() 的垂直平分線方程為
的垂直平分線方程為![]() . ①
. ①
同理直線![]() 的垂直平分線方程為
的垂直平分線方程為![]() . ②
. ②
由①②解得點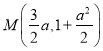 . 又 拋物線
. 又 拋物線![]() 的焦點為
的焦點為![]() 則
則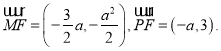 由
由![]() , 可得
, 可得![]() 所以以
所以以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]()
試題解析:
(Ⅰ) 法1:由![]() ,得
,得![]() ,所以
,所以![]() . 所以直線
. 所以直線![]() 的斜率為
的斜率為![]() .
.
因為點![]() 和
和![]() 在拋物線
在拋物線![]() 上, 所以
上, 所以![]() ,
,![]() .
.
所以直線![]() 的方程為
的方程為![]() .
.
因為點![]() 在直線
在直線![]() 上,
上,
所以![]() ,即
,即![]() .
.
同理, ![]() .
.
所以![]() 是方程
是方程![]() 的兩個根.
的兩個根.
所以![]() .
.
又![]() ,
,
所以![]() 為定值.
為定值.
法2:設過點![]() 且與拋物線
且與拋物線![]() 相切的切線方程為
相切的切線方程為![]() ,
,
由![]() 消去
消去![]() 得
得![]() ,
,
由![]() , 化簡得
, 化簡得![]() .
.
所以![]() .
.
由![]() ,得
,得![]() ,所以
,所以![]() .
.
所以直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .
.
所以![]() , 即
, 即![]() .
.
又![]() ,
,
所以![]() 為定值.
為定值.
(Ⅱ) 法1:直線![]() 的垂直平分線方程為
的垂直平分線方程為![]() ,
,
由于![]() ,
,![]() ,
,
所以直線![]() 的垂直平分線方程為
的垂直平分線方程為![]() . ①
. ①
同理直線![]() 的垂直平分線方程為
的垂直平分線方程為![]() . ②
. ②
由①②解得![]() ,
, ![]() ,
,
所以點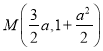 .
.
拋物線![]() 的焦點為
的焦點為![]() 則
則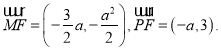
由于![]() ,
,
所以![]()
所以以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]()
另法: 以![]() 為直徑的圓的方程為
為直徑的圓的方程為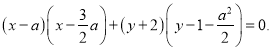
把點![]() 代入上方程,知點
代入上方程,知點![]() 的坐標是方程的解.
的坐標是方程的解.
所以以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]()
法2:設點![]() 的坐標為
的坐標為![]() ,
,
則△![]() 的外接圓方程為
的外接圓方程為![]() ,
,
由于點![]() 在該圓上,
在該圓上,
則![]() ,
,
![]() .
.
兩式相減得![]() , ①
, ①
由(Ⅰ)知![]() ,代入上式得
,代入上式得
![]() ,
,
當![]() 時, 得
時, 得![]() , ②
, ②
假設以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ,則
,則![]() 即
即![]() ,
,
得![]() , ③
, ③
由②③解得![]() ,
,
所以點![]() .
.
當![]() 時, 則
時, 則![]() ,點
,點![]() .
.
所以以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖(1)所示,E為矩形ABCD的邊AD上一點,動點P、Q同時從點B出發,點P以1cm/秒的速度沿折線BE-ED-DC運動到點C時停止,點Q以2cm/秒的速度沿BC運動到點C時停止.設P、Q同時出發t秒時,△BPQ的面積為ycm2.已知y與t的函數關系圖象如圖(2)(其中曲線OG為拋物線的一部分,其余各部分均為線段),則下列結論:①![]() ;②當
;②當![]() 時,
時, ![]() ;③
;③![]() ;④當
;④當![]() 秒時,
秒時, ![]() ∽
∽![]() ;⑤當
;⑤當![]() 的面積為
的面積為![]() 時,時間
時,時間![]() 的值是
的值是![]() 或
或![]() ;其中正確的結論是( )
;其中正確的結論是( )
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為推動乒乓球運動的發展,某乒乓球比賽允許不同協會的運動員組隊參加.現有來自甲協會的運動員![]() 名,其中種子選手
名,其中種子選手![]() 名;乙協會的運動員
名;乙協會的運動員![]() 名,其中種子選手
名,其中種子選手![]() 名.從這
名.從這![]() 名運動員中隨機選擇
名運動員中隨機選擇![]() 人參加比賽.
人參加比賽.
(1)設![]() 為事件“選出的
為事件“選出的![]() 人中恰有
人中恰有![]() 名種子選手,且這
名種子選手,且這![]() 名種子選手來自同一個協會”求事件
名種子選手來自同一個協會”求事件![]() 發生的概率;
發生的概率;
(2)設![]() 為選出的
為選出的![]() 人中種子選手的人數,求隨機變量
人中種子選手的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
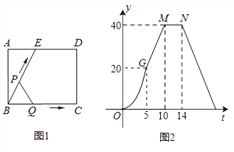
【題目】如圖,已知底角為![]() 的等腰梯形
的等腰梯形![]() ,底邊
,底邊![]() 長為12,腰長為
長為12,腰長為![]() ,當一條垂直于底邊
,當一條垂直于底邊![]() (垂足為
(垂足為![]() )的直線
)的直線![]() 從左至右移動(與梯形
從左至右移動(與梯形![]() 有公共點)時,直線
有公共點)時,直線![]() 把梯形分成兩部分.
把梯形分成兩部分.
(1)令![]() ,試寫出直線右邊部分的面積
,試寫出直線右邊部分的面積![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)在(1)的條件下,令![]() .構造函數
.構造函數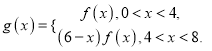
①判斷函數![]() 在
在![]() 上的單調性;
上的單調性;
②判斷函數![]() 在定義域內是否具有單調性,并說明理由.
在定義域內是否具有單調性,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐P-ABCD的底面ABCD是正方形,E,F分別為AC和PB上的點,它的直觀圖,正視圖,側視圖如圖所示.
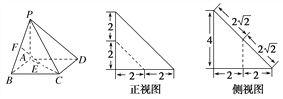
(1)求EF與平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是城市慢行系統的一種模式創新,對于解決民眾出行“最后一公里”的問題特別見效,由于停取方便、租用價格低廉,各色共享單車受到人們的熱捧.某自行車廠為共享單車公司生產新樣式的單車,已知生產新樣式單車的固定成本為20000元,每生產一件新樣式單車需要增加投入100元.根據初步測算,自行車廠的總收益(單位:元)滿足分段函數![]() ,其中
,其中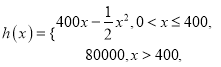
![]() 是新樣式單車的月產量(單位:件),利潤
是新樣式單車的月產量(單位:件),利潤![]() 總收益
總收益![]() 總成本.
總成本.
(1)試將自行車廠的利潤![]() 元表示為月產量
元表示為月產量![]() 的函數;
的函數;
(2)當月產量為多少件時自行車廠的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了制定合理的節電方案,供電局對居民用電進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數據按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
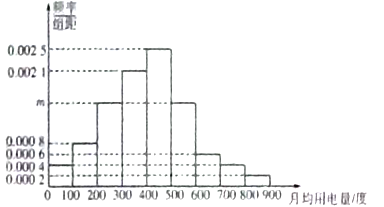
(Ⅰ)求直方圖中![]() 的值并估計居民月均用電量的中位數;
的值并估計居民月均用電量的中位數;
(Ⅱ)現從第8組和第9組的居民中任選取2戶居民進行訪問,則兩組中各有一戶被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將圓![]() 上每一點的縱坐標不變,橫坐標變為原來的
上每一點的縱坐標不變,橫坐標變為原來的![]() ,得曲線C.
,得曲線C.
(Ⅰ)寫出C的參數方程;
(Ⅱ)設直線l: ![]() 與C的交點為P1,P2,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段P1 P2的中點且與l垂直的直線的極坐標方程.
與C的交點為P1,P2,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段P1 P2的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com