
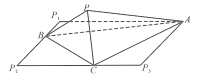
【題目】如圖,在邊長為![]() 的正方形
的正方形![]() 中,線段BC的端點
中,線段BC的端點![]() 分別在邊
分別在邊![]() 、
、![]() 上滑動,且
上滑動,且![]() ,現將
,現將![]() ,
,![]() 分別沿AB,AC折起使點
分別沿AB,AC折起使點![]() 重合,重合后記為點
重合,重合后記為點![]() ,得到三被錐
,得到三被錐![]() .現有以下結論:
.現有以下結論:
①![]() 平面
平面![]() ;
;
②當![]() 分別為
分別為![]() 、
、![]() 的中點時,三棱錐
的中點時,三棱錐![]() 的外接球的表面積為
的外接球的表面積為![]() ;
;
③![]() 的取值范圍為
的取值范圍為![]() ;
;
④三棱錐![]() 體積的最大值為
體積的最大值為![]() .
.
則正確的結論的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根據題意得,折疊成的三棱錐P﹣ABC的三條側棱滿足PA![]() PB、PA
PB、PA![]() PC,由線面垂直的判斷定理得①正確;三棱錐P﹣ABC的外接球的直徑等于以PA、PB、PC為長、寬、高的長方體的對角線長,由此結合AP=2、BP=CP=1,得外接球的半徑R=
PC,由線面垂直的判斷定理得①正確;三棱錐P﹣ABC的外接球的直徑等于以PA、PB、PC為長、寬、高的長方體的對角線長,由此結合AP=2、BP=CP=1,得外接球的半徑R=![]() ,由此得三棱錐P﹣ABC的外接球的體積,故②正確;由題意得
,由此得三棱錐P﹣ABC的外接球的體積,故②正確;由題意得![]() ,
,![]() ,
,![]() ,在
,在![]() 中,由邊長關系得
中,由邊長關系得![]() ,故③正確;由等體積轉化
,故③正確;由等體積轉化![]() 計算即可,故④錯誤.
計算即可,故④錯誤.
由題意得,折疊成的三棱錐P﹣ABC的三條側棱滿足PA![]() PB、PA
PB、PA![]() PC,
PC,
在①中,由PA![]() PB,PA
PB,PA![]() PC,且PB
PC,且PB![]() PC
PC![]() ,所以
,所以![]() 平面
平面![]() 成立,故①正確;
成立,故①正確;
在②中,當![]() 分別為
分別為![]() 、
、![]() 的中點時,三棱錐P﹣ABC的三條側棱兩兩垂直,三棱錐P﹣ABC的外接球直徑等于以PA、PB、PC為長、寬、高的長方體的對角線長,結合AP=2、BP=CP=
的中點時,三棱錐P﹣ABC的三條側棱兩兩垂直,三棱錐P﹣ABC的外接球直徑等于以PA、PB、PC為長、寬、高的長方體的對角線長,結合AP=2、BP=CP=![]() ,
,
得外接球的半徑R=![]() ,所以外接球的表面積為
,所以外接球的表面積為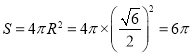 ,故②正確;
,故②正確;
在③中,正方形![]() 的邊長為2,所以
的邊長為2,所以![]() ,
,![]() ,
,![]() ,在
,在![]() 中,由邊長關系得
中,由邊長關系得![]() +
+![]() ,解得
,解得![]() ,故③正確;
,故③正確;
在④中,正方形![]() 的邊長為2,且
的邊長為2,且![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上遞減,無最大值,故④錯誤.
上遞減,無最大值,故④錯誤.
故選:C


科目:高中數學 來源: 題型:
【題目】若橢圓![]() 的焦點在x軸上,離心率為
的焦點在x軸上,離心率為![]() ,依次連接
,依次連接![]() 的四個頂點所得四邊形的面積為40.
的四個頂點所得四邊形的面積為40.
(1)試求![]() 的標準方程;
的標準方程;
(2)若曲線M上任意一點到![]() 的右焦點的距離與它到直線
的右焦點的距離與它到直線![]() 的距離相等,直線
的距離相等,直線![]() 經過
經過![]() 的下頂點和右頂點,
的下頂點和右頂點,![]() ,直線
,直線![]() 與曲線M相交于點P、Q(點P在第一象限內,點Q在第四象限內),設
與曲線M相交于點P、Q(點P在第一象限內,點Q在第四象限內),設![]() 的下頂點是B,上頂點是D,且
的下頂點是B,上頂點是D,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的值域為A,
的值域為A,![]() .
.
(1)當![]() 的為偶函數時,求
的為偶函數時,求![]() 的值;
的值;
(2) 當![]() 時,
時, ![]() 在A上是單調遞增函數,求
在A上是單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,(其中
時,(其中![]() ),若
),若![]() ,且函數
,且函數![]() 的圖象關于點
的圖象關于點![]() 對稱,在
對稱,在![]() 處取 得最小值,試探討
處取 得最小值,試探討![]() 應該滿足的條件.
應該滿足的條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學習小組在研究性學習中,對晝夜溫差大小與綠豆種子一天內出芽數之間的關系進行研究該小組在4月份記錄了1日至6日每天晝夜最高、最低溫度(如圖1),以及浸泡的100顆綠豆種子當天內的出芽數(如圖2).
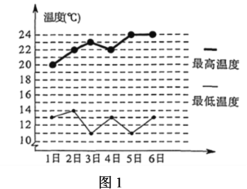
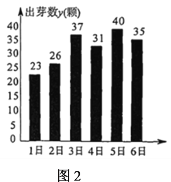
根據上述數據作出散點圖,可知綠豆種子出芽數(顆)和溫差具有線性相關關系.
附: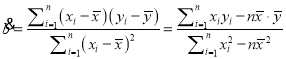 ,
,![]()
(1)求綠豆種子出芽數(顆)關于溫差的回歸方程;
(2)假如4月1日至7日的日溫差的平均值為11℃,估計4月7日浸泡的10000顆綠豆種子一天內的出芽數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 的直線(不與
的直線(不與![]() 軸重合)與橢圓
軸重合)與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,直線
兩點,直線![]() :
:![]() 與
與![]() 軸相交于點
軸相交于點![]() ,過點
,過點![]() 作
作![]() ,垂足為D.
,垂足為D.
(1)求四邊形![]() (
(![]() 為坐標原點)面積的取值范圍;
為坐標原點)面積的取值范圍;
(2)證明直線![]() 過定點
過定點![]() ,并求出點
,并求出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某經銷商從某養殖場購進某品種河蟹,并隨機抽取了 100只進行統計,按重量分類統計,得到頻率分布直方圖如下:
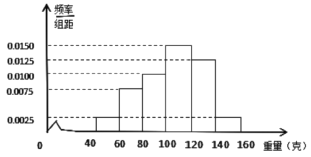
(1)記事件![]() 為“從這批河蟹中任取一只,重量不超過120克”,估計
為“從這批河蟹中任取一只,重量不超過120克”,估計![]() ;
;
(2)試估計這批河蟹的平均重量;
(3)該經銷商按有關規定將該品種河蟹分三個等級,并制定出銷售單價如下:
等級 | 特級 | 一級 | 二級 |
重量 |
|
|
|
單價(元/只) | 40 | 20 | 10 |
試估算該經銷商以每千克至多花多少元(取整)收購這批河蟹,才能獲利?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)若數列{an}是的遞增等差數列,其中的a3=5,且a1,a2,a5成等比數列,
(1)求{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前項的和Tn.
,求數列{bn}的前項的和Tn.
(3)是否存在自然數m,使得![]() <Tn<
<Tn<![]() 對一切n∈N*恒成立?若存在,求出m的值;
對一切n∈N*恒成立?若存在,求出m的值;
若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com