
���}Ŀ����֪���タ![]() ��
��![]() ��ֱ��
��ֱ��![]() �ؒ��タ
�ؒ��タ![]() �������L(zh��ng)��
�������L(zh��ng)��![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2����ֱ��������![]() ������(g��)��c(di��n)�ڒ��タ
������(g��)��c(di��n)�ڒ��タ![]() �ϣ���ֱ����c(di��n)
�ϣ���ֱ����c(di��n)![]() �ęM����(bi��o)��1���^(gu��)�c(di��n)
�ęM����(bi��o)��1���^(gu��)�c(di��n)![]() ��
��![]() �քe�����タ
�քe�����タ![]() ���о������о��ཻ���c(di��n)
���о������о��ཻ���c(di��n)![]() .
.
����ֱ��![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �Ŀv����(bi��o)��
�Ŀv����(bi��o)��
����![]() �����ֵ���˕r(sh��)�c(di��n)
�����ֵ���˕r(sh��)�c(di��n)![]() ������(bi��o).
������(bi��o).
���𰸡���1��![]() ��2����-3.�����ֵҊ(ji��n)������
��2����-3.�����ֵҊ(ji��n)������![]()
��������
��1��(li��n)��![]() ��������c(di��n)�����Ã��c(di��n)���x��ʽ�з�����⼴�ɣ�
��������c(di��n)�����Ã��c(di��n)���x��ʽ�з�����⼴�ɣ�
��2�����O(sh��)�c(di��n)![]() ��
��![]() ��
��![]() ���о�
���о�![]() ��
��![]() ��
��![]() ��
��![]() �����w����η��̵ĸ��Ć�(w��n)�}���ɵ�ֱ��
�����w����η��̵ĸ��Ć�(w��n)�}���ɵ�ֱ��![]() �ķ��̣������c(di��n)
�ķ��̣������c(di��n)![]() �����ɵ��c(di��n)
�����ɵ��c(di��n)![]() �Ŀv����(bi��o)�������}�O(sh��)֪
�Ŀv����(bi��o)�������}�O(sh��)֪![]() ����
����![]() ��������e��ʽ��ʾ��
��������e��ʽ��ʾ��![]() �����ú���(sh��)�����|(zh��)������ֵ.
�����ú���(sh��)�����|(zh��)������ֵ.
�⣺��1��![]() ����Ãɽ��c(di��n)��
����Ãɽ��c(di��n)��![]() ��
��![]() .
.
����![]() ��
��![]() .
.
��2�����O(sh��)�c(di��n)![]() ��
��![]() ��
��![]() .�о�
.�о�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���}�O(sh��)֪![]() ��
��![]() ��
��
��![]() ��
��![]() �Ƿ���
�Ƿ���![]() �ăɸ�������
�ăɸ�������![]() ��
��![]() .
.
��ֱ��![]() ��
��![]() .����?y��n)�ֱ��
.����?y��n)�ֱ��![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() ��
��
����![]() �����c(di��n)
�����c(di��n)![]() �Ŀv����(bi��o)��-3��
�Ŀv����(bi��o)��-3��
�����}�O(sh��)֪![]() ����
����![]() .
.
�t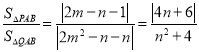 ��
��
��![]() ����
����![]() ��
��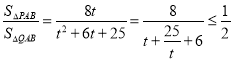 ��
��
��![]() ����
����![]() ��
��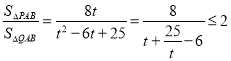 ��
��
��(d��ng)�҃H��(d��ng)![]() ��
��![]() �r(sh��)����̖(h��o)�������˕r(sh��)�c(di��n)
�r(sh��)����̖(h��o)�������˕r(sh��)�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���^(gu��)�E�A![]() ��
�� ![]() �����ҽ��c(di��n)
�����ҽ��c(di��n)![]() �քe��ֱ��
�քe��ֱ��![]() ��
�� ![]() ���E�A��
���E�A��![]() �c
�c![]() ����
����![]() .
.
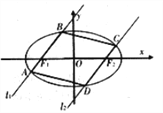
��1�����C����(d��ng)ֱ��![]() ��б��
��б��![]() �cֱ��
�cֱ��![]() ��б��
��б��![]() �����ڕr(sh��)��
�����ڕr(sh��)�� ![]() �鶨ֵ��
�鶨ֵ��
��2������߅��![]() ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
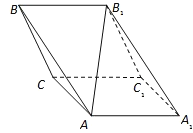
���}Ŀ��б������ABC��A1B1C1����֪��(c��)��BB1C1C�c����ABC��ֱ�ҡ�BCA=90������B1BC=60����BC=BB1=2���������A��B1B��C��30��
��1����AB1�cƽ��BB1C1C���ɽǵ�����ֵ��
��2����ƽ��AA1B1B��(n��i)��һ�c(di��n)P��ʹ�����FP��BB1C���������F������P��ƽ��BB1C���x.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��A
�У��A![]() ����ͨ���̞�
����ͨ���̞�![]() ����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�����S��O�S�ĘO����(bi��o)ϵ�У�ֱ��
�S�����S��O�S�ĘO����(bi��o)ϵ�У�ֱ��![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1����(xi��)���A![]() �ą���(sh��)���̺�ֱ��
�ą���(sh��)���̺�ֱ��![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)�c(di��n)![]() ��
��![]() �ϣ��c(di��n)Q��
�ϣ��c(di��n)Q��![]() �ϣ���
�ϣ���![]() ����Сֵ���˕r(sh��)�c(di��n)
����Сֵ���˕r(sh��)�c(di��n)![]() ��ֱ������(bi��o)��
��ֱ������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ڢ�![]() ����
����![]() ����
����![]() �@����(g��)�l�������xһ��(g��)���a(b��)�������憖(w��n)�}�еęM���ϣ����������(y��ng)�Ć�(w��n)�}.
�@����(g��)�l�������xһ��(g��)���a(b��)�������憖(w��n)�}�еęM���ϣ����������(y��ng)�Ć�(w��n)�}.
��![]() �У���(n��i)��A��B��C�Č�(du��)߅�քe��a��b��c���ҝM��________________��
�У���(n��i)��A��B��C�Č�(du��)߅�քe��a��b��c���ҝM��________________��![]()
![]() ����
����![]() ����e.
����e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M��13�֣�
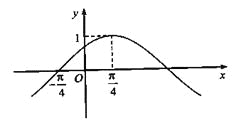
��֪����(sh��)![]() ��
��![]() ������
������![]() �����䲿�ֈD����D��ʾ.
�����䲿�ֈD����D��ʾ.
��I����![]() �Ľ���ʽ��
�Ľ���ʽ��
��II����(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ����ֵ������(y��ng)��
�ϵ����ֵ������(y��ng)��![]() ֵ��
ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�����D��D��ʾ����ݔ��![]() ���t�Д����
���t�Д����![]() �飨 ��
�飨 ��
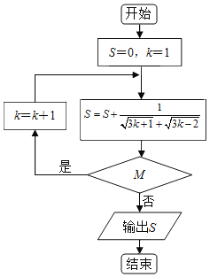
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����^(gu��)���タ![]() ��
��![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() ��ֱ��
��ֱ��![]() �����タ
�����タ![]() ��
��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ��
��![]() ���c(di��n)�����c(di��n)�����タ���о����ɗlֱ������
���c(di��n)�����c(di��n)�����タ���о����ɗlֱ������![]() �c(di��n).
�c(di��n).
��1����(d��ng)ֱ��![]() ƽ����
ƽ����![]() �S�r(sh��)�����c(di��n)
�S�r(sh��)�����c(di��n)![]() ������(bi��o)��
������(bi��o)��
��2����(d��ng)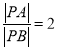 �r(sh��)����ֱ��
�r(sh��)����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
![]() ��
��![]() ��
��![]() ���dž��{(di��o)�f������(sh��)����
���dž��{(di��o)�f������(sh��)����![]() ��ȡֵ������
��ȡֵ������
![]() �O(sh��)
�O(sh��)![]() ����(d��ng)
����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ����
����![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com