已知函數f(x)=(x-a)lnx,(a≥0).
(1)當a=0時,若直線y=2x+m與函數y=f(x)的圖象相切,求m的值;
(2)若f(x)在[1,2]上是單調減函數,求a的最小值;
(3)當x∈[1,2e]時,|f(x)|≤e恒成立,求實數a的取值范圍.(e為自然對數的底).
【答案】
分析:(1)求導函數,利用直線y=2x+m與函數y=f(x)的圖象相切,求切點坐標,即可求m的值;
(2)利用f(x)在[1,2]上是單調減函數,可得
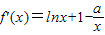
≤0在[1,2]上恒成立,分離參數,求最值,即可求得a的最小值;
(3)當x∈[1,2e]時,|f(x)|≤e恒成立,等價于-e≤(x-a)lnx≤e,|f(x)|≤e恒成立,分離參數,求最值,即可求得實數a的取值范圍.
解答:解:(1)當a=0時,f(x)=xlnx,∴f′(x)=lnx+1
∵直線y=2x+m與函數y=f(x)的圖象相切,∴lnx+1=2,∴x=e
∵f(e)=e,∴切點為(e,e),∴m=-e;
(2)
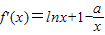
∵f(x)在[1,2]上是單調減函數,
∴
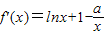
≤0在[1,2]上恒成立
∴a≥xlnx+x在[1,2]上恒成立
令g(x)=xlnx+x,則g′(x)=lnx+2>0
∴g(x)=xlnx+x在[1,2]上單調遞增
∴a≥≥g(2)=2ln2+2
∴a的最小值為2ln2+2;
(3)|f(x)|≤e等價于-e≤(x-a)lnx≤e
∴-
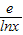
≤x-a≤
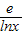
∴x-
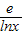
≤a≤x+

設h(x)=x+
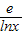
,t(x)=x-
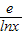
,則t(x)
max≤a≤h(x)
min,
由
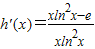
,∵h′(e)=0
令s(x)=xln
2x-e,x∈[1,2e],則s′(x)=ln
2x+lnx>0
∴h(x)在[1,2e]上單調遞增,∴h(x)
min=h(e)=2e,
∵t′(x)=1+
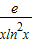
>0,∴t(x)在[1,2e]上單調遞增,
∴t(x)
max=t(2e)=2e-
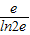
綜上,2e-
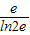
≤a≤2e.
點評:本題考查導數知識的運用,考查導數的幾何意義,考查恒成立問題,分離參數求最值是關鍵.

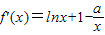 ≤0在[1,2]上恒成立,分離參數,求最值,即可求得a的最小值;
≤0在[1,2]上恒成立,分離參數,求最值,即可求得a的最小值;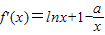
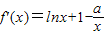 ≤0在[1,2]上恒成立
≤0在[1,2]上恒成立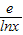 ≤x-a≤
≤x-a≤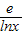
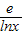 ≤a≤x+
≤a≤x+
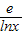 ,t(x)=x-
,t(x)=x-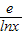 ,則t(x)max≤a≤h(x)min,
,則t(x)max≤a≤h(x)min,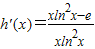 ,∵h′(e)=0
,∵h′(e)=0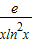 >0,∴t(x)在[1,2e]上單調遞增,
>0,∴t(x)在[1,2e]上單調遞增,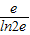
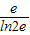 ≤a≤2e.
≤a≤2e.
