【答案】
分析:(1)根據奇函數的性質f(-x)=f(x),已知條件函數f(x)=ax
3+bx
2+cx(a≠0)在x=1處取得極大值2可以推出f′(1)=0和f(1)=2,代入即可求得函數y=f(x)的解析式;
(2)根據題意對于區間[-2,2]上任意兩個自變量的值x
1,x
2都有|f(x
1)-f(x
2)|≤c,將問題轉化為)|f(x
1)-f(x
2)|≤|f(x)
max-f(x)
min|,求出f(x)的最大值和最小值即可;
(3)已知關于p的一元二次方程p
2-2mp+4=0兩個根均大于1,根據根與系數的關系求出m的范圍,利用導數研究函數g(x)的單調性;
解答:解:(1)∵奇函數f(x)=ax
3+bx
2+cx(a≠0)在x=1處取得極大值2,奇函數f(-x)=-f(x),解得b=0,
可得f′(x)=3ax
2+c
由題

,解得

,f(x)=-x
3+3x;
(2)|f(x
1)-f(x
2)|≤|f(x)
max-f(x)
min|=4,
根據(1)可得f(x)=-x
3+3x;
求導得f′(x)=-3x
2+3=-3(x
2-1)令f′(x)=0,可得x=1或-1,
當f′(x)>0即-1<x<1,f(x)為增函數,
當f′(x)<0時即x>1或x<-1,f(x)為減函數,
f(x)在x=1處取極大值f(1)=2,在x=-1處取得極小值f(-1)=-,2;
f(-2)=2,f(2)=-2,
∴f(x)
max=2,f(x)
min=-2,
要使對于區間[-2,2]上任意兩個自變量的值x
1,x
2都有|f(x
1)-f(x
2)|≤c,
∴|f(x
1)-f(x
2)|≤|f(x)
max-f(x)
min|=4,
故c的最小值為4;
(3)p
2-2mp+4=0兩個根均大于1,
則求得
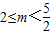
,g(x)=-x
2+3+mlnx,則x>0.
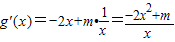
.
而

,則

時,g'(x)>0,
故

是g(x)的單調增區間,

時,g'(x)<0,故

是g(x)的單調減區間.
點評:此題主要考查利用導數研究函數的單調性,考查的知識點比較全面是一道中檔題,這類題是高考的熱點問題;

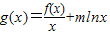 的單調區間.
的單調區間. ,解得
,解得 ,f(x)=-x3+3x;
,f(x)=-x3+3x;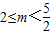 ,g(x)=-x2+3+mlnx,則x>0.
,g(x)=-x2+3+mlnx,則x>0.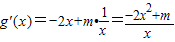 .
. ,則
,則 時,g'(x)>0,
時,g'(x)>0, 是g(x)的單調增區間,
是g(x)的單調增區間, 時,g'(x)<0,故
時,g'(x)<0,故 是g(x)的單調減區間.
是g(x)的單調減區間.

 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案 激活思維優加課堂系列答案
激活思維優加課堂系列答案