
【題目】已知等腰梯形![]() 中(如圖1),
中(如圖1),![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的點,
上的點, ![]() ,現(xiàn)將四邊形
,現(xiàn)將四邊形![]() 沿
沿![]() 折起(如圖2).
折起(如圖2).
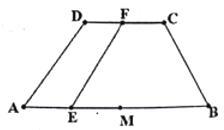
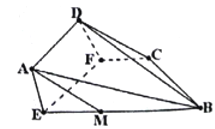
圖1 圖2
⑴求證: ![]() 平面
平面![]() ;
;
⑵在圖2中,若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)連接![]() ,由
,由![]() 可得
可得![]() ,即可證
,即可證![]() ∥
∥![]() 且
且![]() ,然后即可證出四邊形
,然后即可證出四邊形![]() 為平行四邊形,進而可證明
為平行四邊形,進而可證明![]() 平面
平面![]() ;(2)作
;(2)作![]() 于
于![]() ,連接
,連接![]() ,在
,在![]() 中,可得
中,可得![]() ,在
,在![]() 中,可得
中,可得![]() ,結(jié)合
,結(jié)合![]() ,推出
,推出![]() ,再由
,再由![]() ,推出
,推出![]() 平面
平面![]() ,即可得到
,即可得到![]() 為
為![]() 與平面
與平面![]() 所成的角,再根據(jù)余弦定理得出
所成的角,再根據(jù)余弦定理得出![]() ,進而可求出
,進而可求出![]() 的值,即直線
的值,即直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
試題解析:(1)證明:連接![]()
∵![]()
∴![]()
∴![]() ∥
∥![]() ,且
,且![]()
又∵![]() ∥
∥![]() ,且
,且![]()
∴![]() ∥
∥![]() ,且
,且![]()
∴四邊形![]() 為平行四邊形
為平行四邊形
∴![]() ∥
∥![]()
又∵![]() 面
面![]() ,
, ![]() 面
面![]()
∴![]() ∥面
∥面![]()
(2)作![]() 于
于![]() ,連接
,連接![]() ,在
,在![]() 中,易知
中,易知![]() ,而
,而![]()
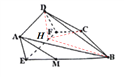
∴![]() ,
, ![]()
在![]() 中,
中, ![]() ,易知
,易知![]()
又∵![]()
∴![]()
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
∴![]()
∴![]()
又∵![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]() 為
為![]() 在平面
在平面![]() 內(nèi)的射影
內(nèi)的射影
∴![]() 為
為![]() 與平面
與平面![]() 所成的角
所成的角
在![]() 中,易知
中,易知![]()
∴![]()
在![]() 中,
中, ![]()
∴![]() ,即
,即![]() 與平面
與平面![]() 的所成的角的正弦值為
的所成的角的正弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,側(cè)棱
,側(cè)棱![]() ,點
,點![]() 分別為棱
分別為棱![]() 的中點,
的中點, ![]() 的重心為
的重心為![]() ,直線
,直線![]() 垂直于平面
垂直于平面![]() .
.
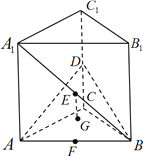
(1)求證:直線![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
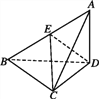
(1)求證:平面ABC⊥平面ACD;
(2)若E為AB中點,求點A到平面CED的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 在圓
在圓![]() 上,
上, ![]() 的坐標分別為
的坐標分別為![]() ,
, ![]() ,線段
,線段![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點
于點![]()
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)圓![]() 與點
與點![]() 的軌跡
的軌跡![]() 交于不同的四個點
交于不同的四個點![]() ,求四邊形
,求四邊形![]() 的面積的最大值及相應(yīng)的四個點的坐標.
的面積的最大值及相應(yīng)的四個點的坐標.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市垃圾處理站每月的垃圾處理量最少為400噸,最多為600噸,月處理成本![]() (元)與月垃圾處理量
(元)與月垃圾處理量![]() (噸)之間的函數(shù)關(guān)系可近似地表示為
(噸)之間的函數(shù)關(guān)系可近似地表示為![]() ,且每處理一噸垃圾得到可利用的資源值為100元.
,且每處理一噸垃圾得到可利用的資源值為100元.
(1)該站每月垃圾處理量為多少噸時,才能使每噸垃圾的平均處理成本最低?
(2)該站每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則需要市財政補貼,至少補貼多少元才能使該站不虧損?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱錐C-ADE的體積;
(II)求證:平面ACE⊥平面CDE;
(III)在線段DE上是否存在一點F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為常數(shù),
為常數(shù), ![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)若![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() ,求
,求![]() 的值;
的值;
(2)當![]() 時,判斷方程
時,判斷方程![]() 是否有實根?若無實根請說明理由,若有實根請給出根的個數(shù).
是否有實根?若無實根請說明理由,若有實根請給出根的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 的方程為
的方程為![]() (
(![]() ,
, ![]() 為常數(shù)).
為常數(shù)).
(1)判斷曲線![]() 的形狀;
的形狀;
(2)設(shè)曲線![]() 分別與
分別與![]() 軸,
軸, ![]() 軸交于點
軸交于點![]() ,
, ![]() (
(![]() ,
, ![]() 不同于原點
不同于原點![]() ),試判斷
),試判斷![]() 的面積
的面積![]() 是否為定值?并證明你的判斷;
是否為定值?并證明你的判斷;
(3)設(shè)直線![]() :
: ![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com