【題目】已知p：方程x2+y2﹣4x+m2＝0表示圓：q：方程
1（m＞0）表示焦點在y軸上的橢圓．
（1）若p為真命題，求實數(shù)m的取值范圍；
（2）若命題p、q有且僅有一個為真，求實數(shù)m的取值范圍．
【答案】（1）﹣2＜m＜2．（2）（﹣2，0]∪[2，3）．
【解析】
（1）把方程x2+y2﹣4x+m2＝0化為（x﹣2）2+y2＝4﹣m2，得到4﹣m2＞0，即可求解；
（2）由方程
1（m＞0）表示焦點在y軸上的橢圓，求得0＜m＜3，再分類討論，列出不等式組，即可求解.
（1）由題意，命題p：方程x2+y2﹣4x+m2＝0，可化得（x﹣2）2+y2＝4﹣m2，
則4﹣m2＞0，解得﹣2＜m＜2，所以實數(shù)m的取值范圍
．
（2）命題q：方程1（m＞0）表示焦點在y軸上的橢圓，則0＜m＜3，
當p為真，q為假時，
，解得﹣2＜m≤0．
當p為假，q為真時，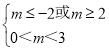
，解得2≤m＜3．
綜上，實數(shù)m的取值范圍為：（﹣2，0]∪[2，3）．
全優(yōu)考典單元檢測卷及歸類總復習系列答案
品學雙優(yōu)卷系列答案
小學期末沖刺100分系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知雙曲線
的兩條漸近線與拋物線
的準線分別交于
，
兩點．若雙曲線
的離心率為
，
的面積為
，
為坐標原點，則拋物線
的焦點坐標為 ( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
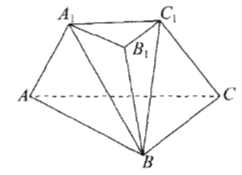
【題目】如圖，在三棱臺
中，底面
是邊長為
的等邊三角形，上、下底面的面積之比為
，側(cè)面
底面，并且
.
（1）平面
平面
，證明：
；
（2）求平面
與平面所成二面角的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某中學2018年的高考考生人數(shù)是2015年高考考生人數(shù)的
倍，為了更好地對比該校考生的升學情況，統(tǒng)計了該校2015年和2018年的高考情況，得到如圖柱狀圖：
則下列結(jié)論正確的是
A. 與2015年相比，2018年一本達線人數(shù)減少
B. 與2015年相比，2018年二本達線人數(shù)增加了
倍
C. 2015年與2018年藝體達線人數(shù)相同
D. 與2015年相比，2018年不上線的人數(shù)有所增加
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點F為拋物線C：y2＝4x的焦點，過點F作斜率為k的直線l與拋物線交于A，B兩點，與準線交于點P，設點D為拋物線準線與x軸的交點．
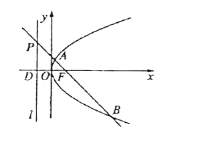
（1）若k＝﹣1，求△DAB的面積；
（2）若
λ
，
μ
，證明：λ+μ為定值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某中學2018年的高考考生人數(shù)是2015年高考考生人數(shù)的倍，為了更好地對比該校考生的升學情況，統(tǒng)計了該校2015年和2018年的高考情況，得到如圖柱狀圖：
則下列結(jié)論正確的是
A. 與2015年相比，2018年一本達線人數(shù)減少
B. 與2015年相比，2018年二本達線人數(shù)增加了倍
C. 2015年與2018年藝體達線人數(shù)相同
D. 與2015年相比，2018年不上線的人數(shù)有所增加
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列命題正確的是（ ）
A.若數(shù)列
、
的極限都存在，且
，則數(shù)列
的極限存在
B.若數(shù)列、的極限都不存在，則數(shù)列
的極限也不存在
C.若數(shù)列、
的極限都存在，則數(shù)列、的極限也存在
D.數(shù)
，若數(shù)列的極限存在，則數(shù)列
的極限也存在
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知曲線 y = x3 + x－2 在點 P0 處的切線
平行于直線
4x－y－1=0，且點 P0 在第三象限,
⑴求P0的坐標;
⑵若直線
, 且 l 也過切點P0 ,求直線l的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
