
已知函數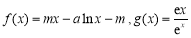 ,其中m,a均為實數.
,其中m,a均為實數.
(1)求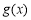 的極值;
的極值;
(2)設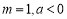 ,若對任意的
,若對任意的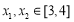
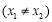 ,
, 恒成立,求
恒成立,求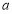 的最小值;
的最小值;
(3)設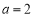 ,若對任意給定的
,若對任意給定的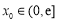 ,在區間
,在區間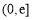 上總存在
上總存在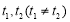 ,使得
,使得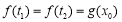 成立,求
成立,求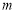 的取值范圍.
的取值范圍.
(1)極大值為1,無極小值.(2)3 ?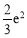 .(3)
.(3) .
.
【解析】
試題分析:(1)求函數極值,先明確定義域為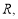 再求其導數為
再求其導數為 .由
.由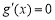 ,得x = 1.分析導數在定義區間符號正負,確定函數先增后減,所以y =
,得x = 1.分析導數在定義區間符號正負,確定函數先增后減,所以y =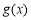 有極大值為1,無極小值.(2)不等式恒成立問題,先化簡不等式
有極大值為1,無極小值.(2)不等式恒成立問題,先化簡不等式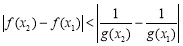 .化簡不等式的難點有兩個,一是絕對值,二是兩個參量
.化簡不等式的難點有兩個,一是絕對值,二是兩個參量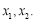 可從函數單調性去絕對值,分析兩個函數,一是
可從函數單調性去絕對值,分析兩個函數,一是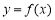 ,二是
,二是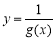 .利用導數可知兩者都是增函數,故原不等式等價于
.利用導數可知兩者都是增函數,故原不等式等價于 ,變量分離調整為
,變量分離調整為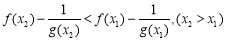 ,這又等價轉化為函數
,這又等價轉化為函數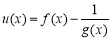 在區間
在區間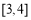 上為減函數,即
上為減函數,即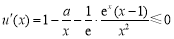 在
在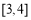 上恒成立.繼續變量分離得
上恒成立.繼續變量分離得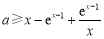 恒成立,即
恒成立,即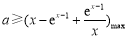 .最后只需求函數
.最后只需求函數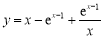 在
在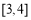 上最大值,就為
上最大值,就為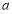 的最小值.(3)本題含義為:對于函數
的最小值.(3)本題含義為:對于函數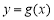 在
在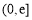 上值域中每一個值,函數
上值域中每一個值,函數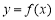 在
在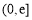 上總有兩個不同自變量與之對應相等.首先求出函數
上總有兩個不同自變量與之對應相等.首先求出函數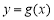 在
在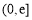 上值域
上值域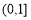 ,然后根據函數
,然后根據函數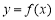 在
在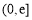 上必須不為單調函數且每段單調區間對應的值域都需包含
上必須不為單調函數且每段單調區間對應的值域都需包含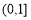 .由
.由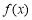 在
在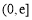 不單調得
不單調得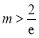 ,由每段單調區間對應的值域都需包含
,由每段單調區間對應的值域都需包含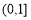 得
得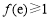 ,
, .
.
試題解析:(1) ,令
,令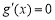 ,得x = 1. 1分
,得x = 1. 1分
列表如下:
x | (?∞,1) | 1 | (1,∞) |
| | 0 | ? |
g(x) | ↗ | 極大值 | ↘ |
∵g(1) = 1,∴y =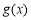 的極大值為1,無極小值. 3分
的極大值為1,無極小值. 3分
(2)當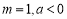 時,
時,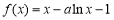 ,
,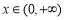 .
.
∵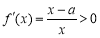 在
在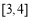 恒成立,∴
恒成立,∴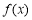 在
在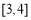 上為增函數. 4分
上為增函數. 4分
設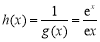 ,∵
,∵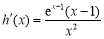 > 0在
> 0在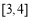 恒成立,
恒成立,
∴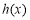 在
在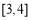 上為增函數. 5分
上為增函數. 5分
設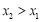 ,則
,則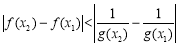 等價于
等價于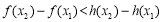 ,
,
即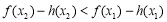 .
.
設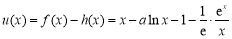 ,則u(x)在
,則u(x)在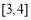 為減函數.
為減函數.
∴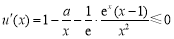 在(3,4)上恒成立 6分
在(3,4)上恒成立 6分
∴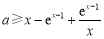 恒成立.
恒成立.
設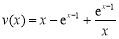 ,∵
,∵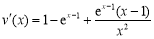 =
=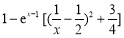 ,x?[3,4],
,x?[3,4],
∴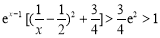 ,∴
,∴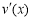 < 0,
< 0,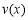 為減函數.
為減函數.
∴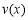 在[3,4]上的最大值為v(3) = 3 ?
在[3,4]上的最大值為v(3) = 3 ?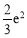 . 8分
. 8分
∴a≥3 ?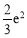 ,∴
,∴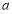 的最小值為3 ?
的最小值為3 ?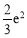 . 9分
. 9分
(3)由(1)知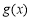 在
在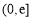 上的值域為
上的值域為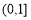 . 10分
. 10分
∵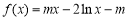 ,
,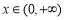 ,
,
當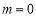 時,
時,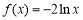 在
在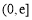 為減函數,不合題意. 11分
為減函數,不合題意. 11分
當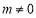 時,
時, ,由題意知
,由題意知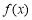 在
在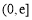 不單調,
不單調,
所以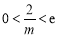 ,即
,即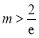 .① 12分
.① 12分
此時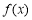 在
在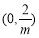 上遞減,在
上遞減,在 上遞增,
上遞增,
∴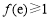 ,即
,即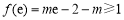 ,解得
,解得 .②
.②
由①②,得 . 13分
. 13分
∵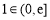 ,∴
,∴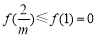 成立. 14分
成立. 14分
下證存在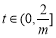 ,使得
,使得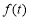 ≥1.
≥1.
取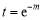 ,先證
,先證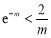 ,即證
,即證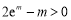 .③
.③
設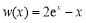 ,則
,則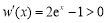 在
在 時恒成立.
時恒成立.
∴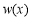 在
在 時為增函數.∴
時為增函數.∴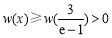 ,∴③成立.
,∴③成立.
再證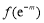 ≥1.
≥1.
∵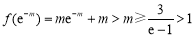 ,∴
,∴ 時,命題成立.
時,命題成立.
綜上所述,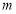 的取值范圍為
的取值范圍為 . 16分
. 16分
考點:函數極值,不等式恒成立


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:高中數學 來源:2013-2014學年江蘇省蘇錫常鎮四市高三教學情況調研二數學試卷(解析版) 題型:填空題
在平面直角坐標系xOy中,已知雙曲線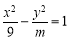 的一個焦點為(5,0),則實數m = .
的一個焦點為(5,0),則實數m = .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)理科數學試卷(解析版) 題型:填空題
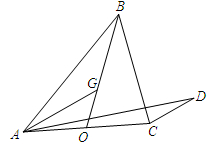
如圖,在△ABC中,BO為邊AC上的中線,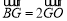 ,設
,設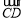 ∥
∥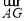 ,若
,若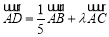
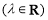 ,則
,則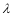 的值為 .
的值為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)文科數學試卷(解析版) 題型:解答題
設函數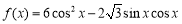 .
.
(1)求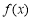 的最小正周期和值域;
的最小正周期和值域;
(2)在銳角△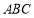 中,角
中,角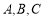 的對邊分別為
的對邊分別為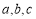 ,若
,若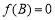 且
且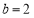 ,
,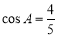 ,求
,求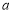 和
和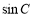 .
.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)文科數學試卷(解析版) 題型:填空題
從甲,乙,丙,丁4個人中隨機選取兩人,則甲乙兩人中有且只有一個被選取的概率為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省鹽城市高三第三次模擬考試數學試卷(解析版) 題型:解答題
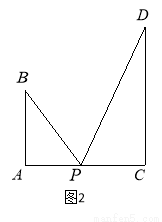
圖1是某斜拉式大橋圖片,為了了解橋的一些結構情況,學校數學興趣小組將大橋的結構進行了簡化,取其部分可抽象成圖2所示的模型,其中橋塔 、
、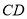 與橋面
與橋面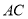 垂直,通過測量得知
垂直,通過測量得知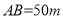 ,
,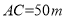 ,當
,當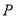 為
為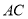 中點時,
中點時,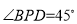 .
.
(1)求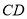 的長;
的長;
(2)試問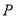 在線段
在線段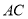 的何處時,
的何處時,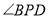 達到最大.
達到最大.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com