
分析 因為題目條件中已知tanα=2,所以轉化為tanα求值.
(1)$\frac{3sinα+2cosα}{sinα-cosα}=\frac{3tanα+2}{tanα-1}$將tanα=2代入即可;
(2)解法1:借助于$\frac{sinα}{cosα}=tanα$和sin2α+cos2α=1得解;解法2:利用cos2α=$\frac{co{s}^{2}α}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1}{1+ta{n}^{2}α}$,“弦”化“切”解之即可.
解答 解:(1)因為tanα=2,所以$\frac{3sinα+2cosα}{sinα-cosα}$=$\frac{3tanα+2}{tanα-1}$=$\frac{3×2+2}{2-1}$=8.
(2)解法1:由$\frac{sinα}{cosα}$=tanα=2,得sinα=2cosα,又sin2α+cos2α=1,
故5cos2α=1,即cos2α=$\frac{1}{5}$,因為α是第三象限角,cosα<0,所以cosα=-$\frac{\sqrt{5}}{5}$.
解法2:因為cos2α=$\frac{co{s}^{2}α}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1}{1+ta{n}^{2}α}$=$\frac{1}{1{+2}^{2}}$=$\frac{1}{5}$,
又因為α是第三象限角,所以cosα<0,
所以cosα=-$\frac{\sqrt{5}}{5}$.
點評 本題考查同角三角函數關系的運用,本題考查sinα、cosα和tanα三者之間的關系.借助于$\frac{sinα}{cosα}=tanα$和sin2α+cos2α=1得解是關鍵,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{1-{m}^{2}}}{m}$ | B. | -$\frac{\sqrt{1-{m}^{2}}}{m}$ | C. | $\frac{m}{\sqrt{1-{m}^{2}}}$ | D. | -$\frac{m}{\sqrt{1-{m}^{2}}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
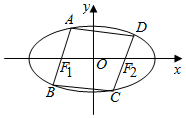 如圖所示,橢圓C:$\frac{{x}^{2}}{4}$+y2=1,左右焦點分別記作F1,F2,過F1,F2分別作直線l1,l2交橢圓AB,CD,且l1∥l2.
如圖所示,橢圓C:$\frac{{x}^{2}}{4}$+y2=1,左右焦點分別記作F1,F2,過F1,F2分別作直線l1,l2交橢圓AB,CD,且l1∥l2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
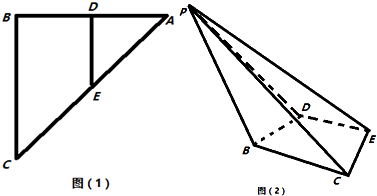
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
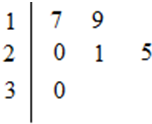 某車間共有12名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
某車間共有12名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com