
【題目】給出下列四個結論:①若![]() 是真命題,則
是真命題,則![]() 可能是真命題;②命題“若
可能是真命題;②命題“若![]() 則
則![]() ”與命題“若
”與命題“若![]() ,則
,則![]() ”互為逆否命題;③若“
”互為逆否命題;③若“![]() 或
或![]() ”是假命題,則“
”是假命題,則“![]() 且
且![]() ”是真命題;④若
”是真命題;④若![]() 是
是![]() 的充分條件,
的充分條件,![]() 是
是![]() 的充分條件,則
的充分條件,則![]() 是
是![]() 的充分條件.其中正確的個數為( )
的充分條件.其中正確的個數為( )
A.1B.2C.3D.4
科目:高中數學 來源: 題型:
【題目】明朝的程大位在《算法統宗》中(1592年),有這么個算法歌訣:三人同行七十稀,五樹梅花廿一枝,七子團圓正半月,除百零五便得知.它的意思是說:求某個數(正整數)的最小正整數值,可以將某數除以3所得的余數乘以70,除以5所得的余數乘以21,除以7所得的余數乘以15,再將所得的三個積相加,并逐次減去105,減到差小于105為止,所得結果就是這個數的最小正整數值.《孫子算經》上有一道極其有名的“物不知數”問題:“今有物不知其數,三三數之余二,五五數之余三,七七數之余二,問物幾何.”用上面的算法歌訣來算,該物品最少是幾件( )
A.21B.22C.23D.24
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“無樁有站”模式的公共自行車日益普及,即傳統自行車加裝智能鎖,實現掃碼租車及刷卡租車、某公司量產了甲、乙兩種款式的公共自行車并投人使用,為了調查消費者對兩種自行車的租賃情況,現隨機抽取這兩種款式的自行車各100輛,分別統計了每輛車在某周內的出租次數,得到甲、乙兩種自行車這周內出租次數的頻數分布表:
甲 | |||||
出租次數(單位:次) |
|
|
|
|
|
頻數 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次數(單位:次) |
|
|
|
|
|
頻數 | 20 | 25 | 25 | 10 | 20 |
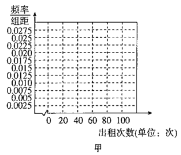
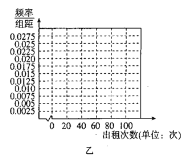
(1)根據頻數分布表,完成上面頻率分布直方圖,并根據頻率分布直方圖比較甲、乙兩種自行車這周內出租次數方差的大小(不必說明理由);
(2)如果兩種自行車每次出租獲得的利潤相同,該公司決定大批量生產其中一種投入某城市使用,請你根據所學的統計知識,給出建議應該生產哪一種自行車,并說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年,北京將實行新的高考方案.新方案規定:語文數學和英語是考生的必考科目,考生還需從物理化學生物歷史地理和政治六個科目中選取三個科目作為選考科目.若一個學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定,例如,學生甲選擇“物理化學和生物”三個選考科目,則學生甲的選考方案確定,“物理化學和生物”為其選考方案.
某校為了解高一年級840名學生選考科目的意向,隨機選取60名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有16人 | 16 | 16 | 8 | 4 | 2 | 2 |
選考方案待確定的有12人 | 8 | 6 | 0 | 2 | 0 | 0 | |
女生 | 選考方案確定的有20人 | 6 | 10 | 20 | 16 | 2 | 6 |
選考方案待確定的有12人 | 2 | 8 | 10 | 0 | 0 | 2 |
(1)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(2)從選考方案確定的16名男生中隨機選出2名,求恰好有一人選“物理化學生物”的概率;
(3)從選考方案確定的16名男生中隨機選出2名,設隨機變量 ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點
為極點![]() ,軸的正半軸為極軸建立極坐標系,圓
,軸的正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 的值;
的值;
(2)直線![]() 與圓
與圓![]() 相交于不同兩點
相交于不同兩點![]() ,
,![]() ,線段
,線段![]() 的中點為
的中點為![]() ,求點
,求點![]() 的軌跡的參數方程.
的軌跡的參數方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 過點
過點 .過點
.過點![]() 做兩條相互垂直的直線
做兩條相互垂直的直線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四點.
四點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直線
,探究:直線![]() 是否過定點?若是,請求出定點坐標;若不是,請說明理由.
是否過定點?若是,請求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年4月23日中國人民海軍建軍70周年.為展現人民海軍70年來的輝煌歷程和取得的巨大成就,我國在山東青島及附近海空舉行盛大的閱兵儀式.我國第一艘航空母艦“遼寧艦”作戰群將參加軍演,要求2艘攻擊型核潛艇一前一后,3艘驅逐艦和3艘護衛艦分列左右,每側3艘,同側不能都是同種艦艇,則艦艇分配方案的方法種數為( )
A.1296B.648C.324D.72
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓Γ:![]() 1(a>b>0)的左、右焦點分別為F1,F2.短軸的兩個頂點與F1,F2構成面積為2的正方形,
1(a>b>0)的左、右焦點分別為F1,F2.短軸的兩個頂點與F1,F2構成面積為2的正方形,
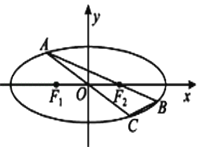
(1)求Γ的方程:
(2)如圖所示,過右焦點F2的直線1交橢圓Γ于A,B兩點,連接AO交Γ于點C,求△ABC面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com