Question

下列四個函數中，圖象如圖1所示的只能是（ ）

A．y=x+ln
B．y=x-ln
C．y=-x+ln
D．y=-x-ln

Answer 1

【答案】分析：由題目中四個答案中的函數解析式，分析判斷其在（0，+∞）上的單調性，然后和已知中的圖象進行比照，即可得到答案．
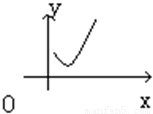
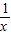解答：解：A中，y=x+lnx，y′=1+，當x＞0時，y′＞0恒成立，故函數在定義域上為增函數，故不符合題目要求；
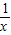B中，y=x-lnx，y′=1-，當0＜x＜1時，y′＜0，x＞1時，y′＞0，故函數在（0，1）上為減函數，在（1，+∞）為增函數，故符合題目要求；
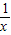C中，y=-x+lnx，y′=-1+，當0＜x＜1時，y′＞0，x＞1時，y′＜0，故函數在（0，1）上為增函數，在（1，+∞）為減函數，故不符合題目要求；
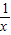D中，y=-x-lnx，y′=-1-，當x＞0時，y′＜0恒成立，故函數在定義域上為減函數，故不符合題目要求；
故選B
點評：本題考查的知識點是函數圖象，函數的單調性，其中根據函數的解析式，利用導數法，分析出函數的單調性是解答本題的關鍵．