
【題目】若存在實常數![]() 和
和![]() ,使得函數
,使得函數![]() 和
和![]() 對其公共定義域上的任意實數x都滿足:
對其公共定義域上的任意實數x都滿足:![]() 和
和![]() 恒成立,則稱此直線
恒成立,則稱此直線![]() 為
為![]() 和
和![]() 的“隔離直線”,已知函數
的“隔離直線”,已知函數![]() ,
,![]() ,
,![]() (
(![]() 為自然對數的底數),則( )
為自然對數的底數),則( )
A.![]() 在
在![]() 內單調遞增;
內單調遞增;
B.![]() 和
和![]() 之間存在“隔離直線”,且
之間存在“隔離直線”,且![]() 的最小值為
的最小值為![]() ;
;
C.![]() 和
和![]() 之間存在“隔離直線”,且
之間存在“隔離直線”,且![]() 的取值范圍是
的取值范圍是![]() ;
;
D.![]() 和
和![]() 之間存在唯一的“隔離直線”
之間存在唯一的“隔離直線”![]() .
.
【答案】ABD
【解析】
令![]() ,利用導數可確定
,利用導數可確定![]() 單調性,得到
單調性,得到![]() 正確;
正確;
設![]() ,
,![]() 的隔離直線為
的隔離直線為![]() ,根據隔離直線定義可得不等式組
,根據隔離直線定義可得不等式組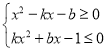 對任意
對任意![]() 恒成立;分別在
恒成立;分別在![]() 和
和![]() 兩種情況下討論
兩種情況下討論![]() 滿足的條件,進而求得
滿足的條件,進而求得![]() 的范圍,得到
的范圍,得到![]() 正確,
正確,![]() 錯誤;
錯誤;
根據隔離直線過![]() 和
和![]() 的公共點,可假設隔離直線為
的公共點,可假設隔離直線為![]() ;分別討論
;分別討論![]() 、
、![]() 和
和![]() 時,是否滿足
時,是否滿足![]() 恒成立,從而確定
恒成立,從而確定![]() ,再令
,再令![]() ,利用導數可證得
,利用導數可證得![]() 恒成立,由此可確定隔離直線,則
恒成立,由此可確定隔離直線,則![]() 正確.
正確.
對于![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
![]() ,
,![]() 在
在![]() 內單調遞增,
內單調遞增,
![]() 正確;
正確;
對于![]() ,設
,設![]() ,
,![]() 的隔離直線為
的隔離直線為![]() ,
,
則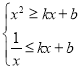 對任意
對任意![]() 恒成立,即
恒成立,即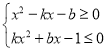 對任意
對任意![]() 恒成立.
恒成立.
由![]() 對任意
對任意![]() 恒成立得:
恒成立得:![]() .
.
⑴若![]() ,則有
,則有![]() 符合題意;
符合題意;
⑵若![]() 則有
則有![]() 對任意
對任意![]() 恒成立,
恒成立,
![]() 的對稱軸為
的對稱軸為![]() ,
,![]() ,
,![]() ;
;
又![]() 的對稱軸為
的對稱軸為![]() ,
,![]() ;
;
即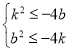 ,
,![]() ,
,![]() ;
;
同理可得:![]() ,
,![]() ;
;
綜上所述:![]() ,
,![]() ,
,![]() 正確,
正確,![]() 錯誤;
錯誤;
對于![]() ,
,![]() 函數
函數![]() 和
和![]() 的圖象在
的圖象在![]() 處有公共點,
處有公共點,
![]() 若存在
若存在![]() 和
和![]() 的隔離直線,那么該直線過這個公共點.
的隔離直線,那么該直線過這個公共點.
設隔離直線的斜率為![]() ,則隔離直線方程為
,則隔離直線方程為![]() ,即
,即![]() ,
,
則![]() 恒成立,
恒成立,
若![]() ,則
,則![]() 不恒成立.
不恒成立.
若![]() ,令
,令![]() ,對稱軸為
,對稱軸為![]()
![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,故
,故![]() 時,
時,![]() 不恒成立.
不恒成立.
若![]() ,
,![]() 對稱軸為
對稱軸為![]() ,
,
若![]() 恒成立,則
恒成立,則![]() ,解得:
,解得:![]() .
.
此時直線方程為:![]() ,
,
下面證明![]() ,
,
令![]() ,則
,則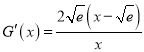 ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
![]() 當
當![]() 時,
時,![]() 取到極小值,也是最小值,即
取到極小值,也是最小值,即![]() ,
,
![]() ,即
,即![]() ,
,
![]() 函數
函數![]() 和
和![]() 存在唯一的隔離直線
存在唯一的隔離直線![]() ,
,![]() 正確.
正確.
故選:![]() .
.


科目:高中數學 來源: 題型:
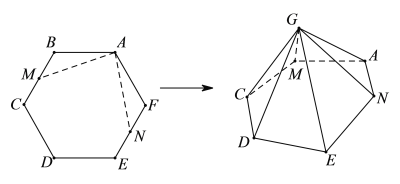
【題目】如圖,六邊形![]() 的六個內角均相等,
的六個內角均相等,![]() ,M,N分別是線段
,M,N分別是線段![]() ,
,![]() 上的動點,且滿足
上的動點,且滿足![]() ,現將
,現將![]() ,
,![]() 折起,使得B,F重合于點G,則二面角
折起,使得B,F重合于點G,則二面角![]() 的余弦值的取值范圍是______.
的余弦值的取值范圍是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了治療某種疾病,某科研機構研制了甲、乙兩種新藥,為此進行白鼠試驗.試驗方案如下:每一輪選取兩只白鼠對藥效進行對比試驗.對于兩只白鼠,隨機選一只施以甲藥,另一只施以乙藥一輪的治療結果得出后,再安排下一輪試驗.4輪試驗后,就停止試驗.甲、乙兩種藥的治愈率分別是![]() 和
和![]() .
.
(1)若![]() ,求2輪試驗后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率;
,求2輪試驗后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率;
(2)已知A公司打算投資甲、乙這兩種新藥的試驗耗材費用,甲藥和乙藥一次試驗耗材花費分別為3千元和![]() 千元,每輪試驗若甲、乙兩種藥都治愈或都沒有治愈,則該科研機構和A公司各承擔該輪試驗耗材總費用的50%;若甲藥治愈,乙藥未治愈,則A公司承擔該輪試驗耗材總費用的75%,其余由科研機構承擔,若甲藥未治愈,乙藥治愈,則A公司承擔該輪試驗耗材總費用的25%,其余由科研機構承擔.以A公司每輪支付試驗耗材費用的期望為標準,求A公司4輪試驗結束后支付試驗耗材最少費用為多少元?
千元,每輪試驗若甲、乙兩種藥都治愈或都沒有治愈,則該科研機構和A公司各承擔該輪試驗耗材總費用的50%;若甲藥治愈,乙藥未治愈,則A公司承擔該輪試驗耗材總費用的75%,其余由科研機構承擔,若甲藥未治愈,乙藥治愈,則A公司承擔該輪試驗耗材總費用的25%,其余由科研機構承擔.以A公司每輪支付試驗耗材費用的期望為標準,求A公司4輪試驗結束后支付試驗耗材最少費用為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖、“90后”從事互聯網行業崗位分布條形圖,則下列結論中正確的是( )
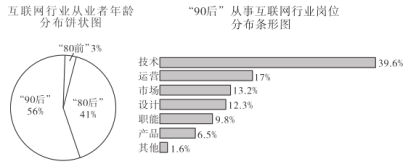
注:“90后”指1990年及以后出生的人,“80后”指1980-1989年之間出生的人,“80前”指1979年及以前出生的人.
A.互聯網行業從業人員中“90后”占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的20%
C.互聯網行業中從事運營崗位的人數“90后”比“80前”多
D.互聯網行業中從事技術崗位的人數“90后”比“80后”多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 只能同時滿足下列三個條件中的兩個:①函數
只能同時滿足下列三個條件中的兩個:①函數![]() 的最大值為2;②函數
的最大值為2;②函數![]() 的圖象可由
的圖象可由![]() 的圖象平移得到;③函數
的圖象平移得到;③函數![]() 圖象的相鄰兩條對稱軸之間的距離為
圖象的相鄰兩條對稱軸之間的距離為![]() .
.
(1)請寫出這兩個條件序號,并求出![]() 的解析式;
的解析式;
(2)求方程![]() 在區間
在區間![]() 上所有解的和.
上所有解的和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com