
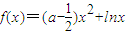 .(a∈R)
.(a∈R)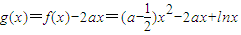 ,則g(x)的定義域為(0,+∞).證g(x)<0在區間(1,+∞)上恒成立即得證.求出g′(x)分區間討論函數的增減性得到函數的極值,利用極值求出a的范圍即可.
,則g(x)的定義域為(0,+∞).證g(x)<0在區間(1,+∞)上恒成立即得證.求出g′(x)分區間討論函數的增減性得到函數的極值,利用極值求出a的范圍即可.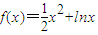 ,
,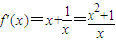 .
.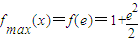 ,
,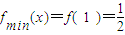
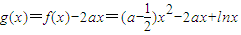 ,則g(x)的定義域為(0,+∞).
,則g(x)的定義域為(0,+∞).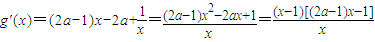 .
.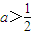 ,令g'(x)=0,得極值點x1=1,
,令g'(x)=0,得極值點x1=1,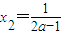 .
.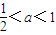 時,在(x2,+∞)上有g'(x)>0.
時,在(x2,+∞)上有g'(x)>0.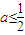 ,則有2a-1≤0,此時在區間(1,+∞)上恒有g'(x)<0.
,則有2a-1≤0,此時在區間(1,+∞)上恒有g'(x)<0.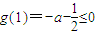
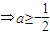 .
.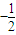 ,
, ].
].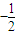 ,
, ]時,函數f(x)的圖象恒在直線y=2ax下方.
]時,函數f(x)的圖象恒在直線y=2ax下方.

 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數學 來源:2012-2013學年山東省濟寧市汶上一中高二(下)期末數學試卷(理科)(解析版) 題型:解答題
 ,其中a∈R.
,其中a∈R.查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省南京市高三第二次模擬考試數學卷 題型:填空題
已知函數f(x)= 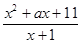 (a∈R),若對于任意的X∈N*,f(x)≥3恒成立,則a的取值范圍是___
(a∈R),若對于任意的X∈N*,f(x)≥3恒成立,則a的取值范圍是___
查看答案和解析>>
科目:高中數學 來源:2009-2010學年江蘇省南京九中高三(上)期中數學練習試卷(文科)(解析版) 題型:填空題
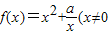 ,常數a∈R),若函數f(x)在x∈[2,+∞)上是增函數,則a的取值范圍是 .
,常數a∈R),若函數f(x)在x∈[2,+∞)上是增函數,則a的取值范圍是 .查看答案和解析>>
科目:高中數學 來源:2012-2013學年北京三十九中高三(上)期中數學試卷(理科)(解析版) 題型:解答題
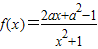 ,其中a∈R.
,其中a∈R.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com