
【題目】如圖,在底面是直角梯形的四棱錐S-ABCD中,![]() 面
面![]() .
.

(1)求四棱錐S-ABCD的體積;
(2)求證:面![]()
![]()
(3)求SC與底面ABCD所成角的正切值。
【答案】(1)![]() ;(2)見解析(3)
;(2)見解析(3)![]() .
.
【解析】
(1)根據梯形的面積公式及四棱錐的體積公式直接求值即可.
(2)先由SA⊥面ABCD,可得SA⊥BC,再由AB⊥BC ,得BC⊥平面SAB,從而證得平面SAB⊥平面SBC.
(3)找到線面角是解決問題的關鍵.連接AC ∵SA⊥面ABCD
∴∠SCA為SC與底面ABCD所成的角,然后解三角形即可.
證明:(1)S梯形ABCD=![]() (AD+BC)·AB=
(AD+BC)·AB=![]() (
(![]() +1)×1=
+1)×1=![]()
VS-ABCD=![]() ×
×![]() ×1=
×1=![]() ……………2分
……………2分
(2)∵SA⊥面ABCD ∴SA⊥BC……………………………………3分
又AB⊥BC ∴BC⊥平面SAB
∴平面SAB⊥平面SBC……………………………………5分
(3)連接AC ∵SA⊥面ABCD
∴∠SCA為SC與底面ABCD所成的角……………………………………7分
在Rt△ABC中,AC=![]() =
=![]()
在Rt△SAC中,tan∠SCA=![]() =
=![]() =
=![]() ……………………………………9分
……………………………………9分


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某學校舉行了一次安全教育知識競賽,競賽的原始成績采用百分制,已知高三學生的原始成績均分布在![]() 內,發布成績使用等級制,各等級劃分標準見表.
內,發布成績使用等級制,各等級劃分標準見表.
原始成績 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等級 | 優秀 | 良好 | 及格 | 不及格 |
為了解該校高三年級學生安全教育學習情況,從中抽取了![]() 名學生的原始成績作為樣本進行統計,按照
名學生的原始成績作為樣本進行統計,按照![]() 的分組作出頻率分布直方圖如圖所示,其中等級為不及格的有5人,優秀的有3人.
的分組作出頻率分布直方圖如圖所示,其中等級為不及格的有5人,優秀的有3人.
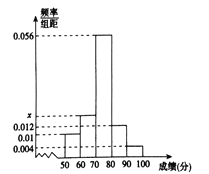
(1)求![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)根據樣本估計總體的思想,以事件發生的頻率作為相應事件發生的概率,若該校高三學生共1000人,求競賽等級在良好及良好以上的人數;
(3)在選取的樣本中,從原始成績在80分以上的學生中隨機抽取2名學生進行學習經驗介紹,求抽取的2名學生中優秀等級的學生恰好有1人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,已知圓![]() 的圓心坐標為
的圓心坐標為![]() ,半徑為
,半徑為![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數)
為參數)
(1)求圓![]() 和直線
和直線![]() 的極坐標方程;
的極坐標方程;
(2)點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 與圓
與圓![]() 相較于
相較于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
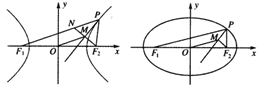
【題目】如圖,P是雙曲線![]() (a>0,b>0,xy≠0)上的動點,F1,F2是雙曲線的焦點,M是∠F1PF2的平分線上一點,且
(a>0,b>0,xy≠0)上的動點,F1,F2是雙曲線的焦點,M是∠F1PF2的平分線上一點,且![]() .某同學用以下方法研究|OM|:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得|OM|=
.某同學用以下方法研究|OM|:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得|OM|=![]() |NF1|=…=a。類似地:P是橢圓
|NF1|=…=a。類似地:P是橢圓![]() (a>b>0,xy≠0)上的動點,F1,F2是橢圓的焦點,M是∠F1PF2的平分線上一點,且
(a>b>0,xy≠0)上的動點,F1,F2是橢圓的焦點,M是∠F1PF2的平分線上一點,且![]() ,則|OM|的取值范圍是________.
,則|OM|的取值范圍是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com