
【題目】橢圓![]() 的焦距是
的焦距是![]() ,長軸長是短軸長3倍,任作斜率為
,長軸長是短軸長3倍,任作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(如圖所示),且點
兩點(如圖所示),且點![]() 在直線
在直線![]() 的左上方.
的左上方.
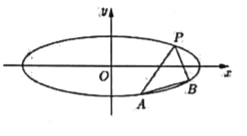
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面積;
的面積;
(3)證明:![]() 的內切圓的圓心在一條定直線上。
的內切圓的圓心在一條定直線上。
【答案】(1)![]()
(2)![]()
(3)![]() 的內切圓的圓心在一條定直線
的內切圓的圓心在一條定直線![]() 上
上
【解析】
(1)由題意求出橢圓方程中的![]() ,得解;
,得解;
(2)分別利用弦長公式及點到直線的距離公式求出三角形的底與高,再利用三角形面積公式求解即可;
(3)先證明![]() ,從而可得
,從而可得![]() 的角平分線平行
的角平分線平行![]() 軸,從而可證
軸,從而可證![]() 的內切圓的圓心在一條定直線上.
的內切圓的圓心在一條定直線上.
解:(1)由題意知:![]() ,得
,得![]() ,又
,又![]() ,
,
所以![]() ,
,
故橢圓![]() 的方程為:
的方程為:![]() ;
;
(2)設直線![]() 的方程為:
的方程為:![]() ,代入橢圓方程可得:
,代入橢圓方程可得:![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,
所以![]() ,
,
又![]() ,解得
,解得![]() 或
或![]() ,
,
由題意可得![]() ,
,
故![]() 所在直線方程為
所在直線方程為![]() ,即
,即![]() ,
,
所以點![]() 到直線
到直線![]() 的距離
的距離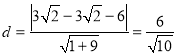 ,
,
故![]() 的面積為
的面積為![]() ;
;
(3)設直線![]() 的方程為:
的方程為:![]() ,代入橢圓方程可得:
,代入橢圓方程可得:![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,
所以 =
=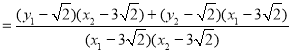 ,
,
又![]()
![]()
![]()
![]()
![]() ,
,
即 ![]() ,所以
,所以![]() 的角平分線平行
的角平分線平行![]() 軸,
軸,
故![]() 的內切圓的圓心在一條定直線
的內切圓的圓心在一條定直線![]() 上.
上.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|﹣|x﹣5|.
(1)當a=2時,求證:﹣3≤f(x)≤3;
(2)若關于x的不等式f(x)≤x2﹣8x+20在R恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]() 相外切,且與直線
相外切,且與直線![]() 相切.
相切.
(1)記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,求
,求![]() 的方程;
的方程;
(2)過點![]() 的兩條直線
的兩條直線![]() 與曲線
與曲線![]() 分別相交于點
分別相交于點![]() 和
和![]() ,線段
,線段![]() 和
和![]() 的中點分別為
的中點分別為![]() .如果直線
.如果直線![]() 與
與![]() 的斜率之積等于1,求證:直線
的斜率之積等于1,求證:直線![]() 經過定點.
經過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,設
,設![]() 為線段
為線段![]() 的中點.則在
的中點.則在![]() 翻折過程中,給出如下結論:
翻折過程中,給出如下結論:
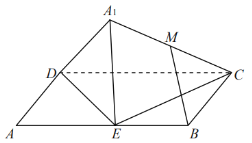
①當![]() 不在平面
不在平面![]() 內時,
內時,![]() 平面
平面![]() ;
;
②存在某個位置,使得![]() ;
;
③線段![]() 的長是定值;
的長是定值;
④當三棱錐![]() 體積最大時,其外接球的表面積為
體積最大時,其外接球的表面積為![]() .
.
其中,所有正確結論的序號是______.(請將所有正確結論的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 與定點
與定點![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數
的距離的比是常數![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過坐標原點![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() ,
,![]() 兩點,軌跡
兩點,軌跡![]() 上異于
上異于![]() ,
,![]() 的點
的點![]() 滿足直線
滿足直線![]() 的斜率為
的斜率為![]() .
.
(ⅰ)證明:直線![]() 與
與![]() 的斜率之積為定值;
的斜率之積為定值;
(ⅱ)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省即將實行新高考,不再實行文理分科.某校為了研究數學成績優秀是否對選擇物理有影響,對該校2018級的1000名學生進行調查,收集到相關數據如下:
(1)根據以上提供的信息,完成![]() 列聯表,并完善等高條形圖;
列聯表,并完善等高條形圖;
選物理 | 不選物理 | 總計 | |
數學成績優秀 | |||
數學成績不優秀 | 260 | ||
總計 | 600 | 1000 |
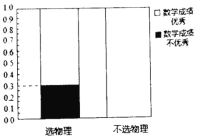
(2)能否在犯錯誤的概率不超過0.05的前提下認為數學成績優秀與選物理有關?
附: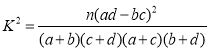
臨界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為坐標原點,動點
為坐標原點,動點![]() 在圓
在圓![]() 上,過
上,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,點
,點![]() 滿足
滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 上的點
上的點![]() 滿足
滿足![]() .過點
.過點![]() 作直線
作直線![]() 垂直于線段
垂直于線段![]() 交
交![]() 于點
于點![]() .
.
(ⅰ)證明:![]() 恒過定點;
恒過定點;
(ⅱ)設線段![]() 交
交![]() 于點
于點![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為助力湖北新冠疫情后的經濟復蘇,某電商平臺為某工廠的產品開設直播帶貨專場.為了對該產品進行合理定價,用不同的單價在平臺試銷,得到如下數據:
單價 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根據以上數據,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若該產品成本是4元/件,假設該產品全部賣出,預測把單價定為多少時,工廠獲得最大利潤?
(參考公式:回歸方程![]() ,其中
,其中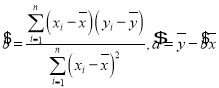 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com