過點A(4,2),且在兩坐標軸上截距相等的直線方程 .
【答案】
分析:當直線過原點時,求出斜率,斜截式寫出直線方程,并化為一般式.當直線不過原點時,設直線的方程為 x+y+m=0,把A(4,2)代入直線的方程,求出m值,可得直線方程.
解答:解:當直線過原點時,斜率等于
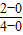
=

,故直線的方程為y=

x,即 x-2y=0.
當直線不過原點時,設直線的方程為 x+y+m=0,把A(4,2)代入直線的方程得 m=-6,
故求得的直線方程為 x+y-6=0,綜上,滿足條件的直線方程為 x-2y=0或 x+y-6=0.
故答案為:x-2y=0或 x+y-6=0.
點評:本題考查求直線方程的方法,待定系數法求直線的方程是一種常用的方法,體現了分類討論的數學思想.

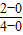 =
= ,故直線的方程為y=
,故直線的方程為y= x,即 x-2y=0.
x,即 x-2y=0.
