
(本小題滿分l2分) 已知函數f(x)=ax3+bx2-3x在x=±1處取得極值.
(1)求函數f(x)的解析式;
(2)求證:對于區間[-1,1]上任意兩個自變量的值x1,x2,都有|f(x1)-f(x2)|≤4;
(3)若過點A(1,m)(m≠-2)可作曲線y=f(x)的三條切線,求實數m的取值范圍.
(1) ;(2)略;(3)
;(2)略;(3)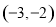 .
.
【解析】
試題分析:(1)利用導數與極值的關系可列出關于 的二元一次方程組,從而可求出函數的解析式.由題意可知
的二元一次方程組,從而可求出函數的解析式.由題意可知 ,依題意可知
,依題意可知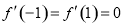 ,從而可列方程組
,從而可列方程組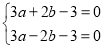 ,解得
,解得 ,所以函數
,所以函數 的解析式為
的解析式為 ;
;
(2)利用函數單調性求最值的方法,先判斷函數 在區間
在區間 上的單調性,并求出函數
上的單調性,并求出函數 在區間
在區間 上的最大值與最小值之差,從而命題可得證明.由(1)可知
上的最大值與最小值之差,從而命題可得證明.由(1)可知 ,令
,令 ,解得
,解得 ,即函數
,即函數 在區間
在區間 上為單調遞減,所以
上為單調遞減,所以 ,
, ,因為對于區間
,因為對于區間 上的任意兩個自變量的值
上的任意兩個自變量的值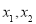 ,
,
都有 ,所以命題得證;
,所以命題得證;
(3)由(1)可知 , 由曲線方程
, 由曲線方程 可知點
可知點 不在曲線上.
不在曲線上.
設切點為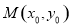 ,則
,則
因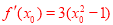 ,故切線的斜率為
,故切線的斜率為 ,整理得
,整理得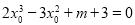 ,
,
因為過點 可作曲線的三條切線,所以關于
可作曲線的三條切線,所以關于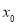 的方程
的方程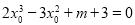 有三個實根,
有三個實根,
設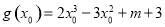 ,則
,則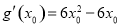 ,由
,由 ,得
,得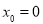 或
或 ,
,
所以 在
在 ,
,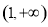 上單調遞增,在
上單調遞增,在 上單調遞減,因此函數
上單調遞減,因此函數 的極值點為0、1,
的極值點為0、1,
所以關于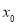 的方程
的方程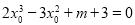 有三個實根的充要條件是
有三個實根的充要條件是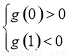 ,解得
,解得 .
.
故所求實數 的取值范圍為
的取值范圍為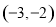 .
.
試題解析:(1)f′(x)=3ax2+2bx-3,依題意,f′(1)=f′(-1)=0,
即 解得a=1,b=0.∴f(x)=x3-3x.-------3分
解得a=1,b=0.∴f(x)=x3-3x.-------3分
(2)∵f(x)=x3-3x,∴f′(x)= 3x2-3=3(x+1)(x-1),
當-1<x<1時,f′(x)<0,故f(x)在區間[-1, 1]上為減函數,fmax(x)=f(-1)=2,fmin(x)=f(1)=-2
∵對于區間[-1,1]上任意兩個自變量的值x1,x2,
都有|f(x1)-f(x2)|≤|fmax(x) -fmin(x)|,所以|f(x1)-f(x2)|≤2-(-2)=4 -----7分
(3)f′(x)=3x2-3=3(x+1)(x-1),
∵曲線方程為y=x3-3x,∴點A(1,m)不在曲線上.
設切點為M(x0,y0),則點M的坐標滿足 因
因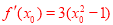 ,
,
故切線的斜率為 ,整理得
,整理得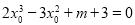 ,
,
因為過點 可作曲線的三條切線,所以關于
可作曲線的三條切線,所以關于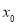 的方程
的方程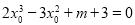 有三個實根,
有三個實根,
設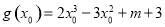 ,則
,則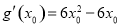 ,由
,由 ,得
,得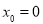 或
或 ,
,
所以 在
在 ,
,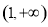 上單調遞增,在
上單調遞增,在 上單調遞減,因此函數
上單調遞減,因此函數 的極值點為0、1,
的極值點為0、1,
所以關于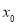 的方程
的方程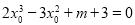 有三個實根的充要條件是
有三個實根的充要條件是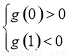 ,解得
,解得 .
.
故所求實數 的取值范圍為
的取值范圍為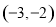 . 12分
. 12分
考點:1.導函數的應用;2.利用函數最值證明不等式.


科目:高中數學 來源: 題型:
| A、?x0∈R,log2x0>0 | B、?x0∈R,log2x0≥0 | C、?x∈R,log2x≥0 | D、?x∈R,log2x>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、484種 | B、552種 | C、560種 | D、612種 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 | 3 | 4 |
| 4 | 3 | 1 | 2 |
| 2 | 1 | 4 | 3 |
| 3 | 4 | 2 | 1 |
| A、432 | B、576 |
| C、720 | D、864 |
查看答案和解析>>
科目:高中數學 來源:2015屆西藏拉薩中學高三第三次月考理科數學試卷(解析版) 題型:解答題
(本題滿分12分)已知函數 ,x∈R.(其中m為常數).
,x∈R.(其中m為常數).
(1)當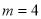 時,求函數的極值點和極值;
時,求函數的極值點和極值;
(2)若函數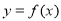 在區間(0,+∞)上有兩個極值點,求實數
在區間(0,+∞)上有兩個極值點,求實數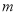 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com