
分析 (Ⅰ)先求出f(x)定義域為(0,1)∪(1,+∞),$f'(x)=\frac{{\frac{b}{x}(x-1)-(a+blnx)}}{{{{(x-1)}^2}}}$,由函數f(x)在點 (2,f (2)) 處切線的斜率為-$\frac{1}{2}$-ln 2,且函數過點(4,$\frac{1+2ln2}{3}$),列出方程組求出a,b,從而$f'(x)=\frac{{\frac{1}{x}(x-1)-(1+lnx)}}{{{{(x-1)}^2}}}=\frac{{-\frac{1}{x}-lnx}}{{{{(x-1)}^2}}}$記$h(x)=-\frac{1}{x}-lnx$,則$h'(x)=\frac{1}{x^2}-\frac{1}{x}=\frac{1-x}{x^2}$,利用導數性質能求出函數 f (x)的單調區間.
(Ⅱ)原問題轉化為f(x)<g(x)在x∈(0,1)上恒成立,f(x)>g(x)在x∈(1,+∞)上恒成立,從而$φ(x)=1+lnx-(1-\frac{1}{x})k>0$在x∈(0,1)∪(1,+∞)上恒成立,由此利用導數性質能求出k的最大值.
解答 解:(Ⅰ)∵函數f(x)=$\frac{a+blnx}{x-1}$(a,b∈R),
∴f(x)定義域為(0,1)∪(1,+∞),
$f'(x)=\frac{{\frac{b}{x}(x-1)-(a+blnx)}}{{{{(x-1)}^2}}}$…(1分)
∵函數f(x)在點 (2,f (2)) 處切線的斜率為-$\frac{1}{2}$-ln 2,且函數過點(4,$\frac{1+2ln2}{3}$).
∴$\left\{\begin{array}{l}f'(2)=\frac{b}{2}-a-bln2=-\frac{1}{2}-ln2\\ f(4)=\frac{a+bln4}{3}=\frac{1+2ln2}{3}\end{array}\right.$…(2分)
∴$\left\{\begin{array}{l}a+bln2-\frac{b}{2}=\frac{1}{2}+ln2\\ a+2bln2=1+2ln2\end{array}\right.$,
∴$\left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$…(3分)
∴$f'(x)=\frac{{\frac{1}{x}(x-1)-(1+lnx)}}{{{{(x-1)}^2}}}=\frac{{-\frac{1}{x}-lnx}}{{{{(x-1)}^2}}}$
記$h(x)=-\frac{1}{x}-lnx$,則$h'(x)=\frac{1}{x^2}-\frac{1}{x}=\frac{1-x}{x^2}$,
h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,
h(x)≤h(1)=-1<0…(4分)
∴$f'(x)=\frac{{-\frac{1}{x}-lnx}}{{{{(x-1)}^2}}}<0$恒成立,
∴f(x)在(0,1)上單調遞減,在(1,+∞)上單調遞減.…(5分)
(Ⅱ)由題得,原問題轉化為f(x)<g(x)在x∈(0,1)上恒成立,
f(x)>g(x)在x∈(1,+∞)上恒成立,…(6分)
即$φ(x)=1+lnx-(1-\frac{1}{x})k>0$在x∈(0,1)∪(1,+∞)上恒成立,…(7分)
$φ'(x)=\frac{1}{x}-\frac{k}{x^2}=\frac{x-k}{x^2}$,
∴φ(x)在(0,1),(1,k)上單調遞減,(k,+∞)上單調遞增,…(8分)
當x∈(0,1)時,φ(x)>φ(1)=1>0…(9分)
當x∈(1,+∞)時,φ(x)≥φ(k)=lnk-k+2,∴lnk-k+2>0…(10分)
記Φ(k)=lnk-k+2,則$Φ'(k)=\frac{1}{k}-1=\frac{1-k}{k}≤0$恒成立,
Φ(k)在k∈[1,+∞)上是減函數,…(11分)
Φ(3)=ln3-1>0,Φ(4)=ln4-2<0,
∴k的最大值為3.…(12分)
點評 本題考查實數值的求法,考查函數的單調區間的求法,考查實數的最大值的求法,是中檔題,解題時要認真審題,注意導數性質、構造法的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
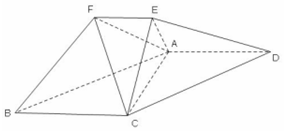 在如圖所示的幾何體中,平面ACE⊥平面ABCD,四邊形ABCD 為平行四邊形,
在如圖所示的幾何體中,平面ACE⊥平面ABCD,四邊形ABCD 為平行四邊形,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com