
【題目】隨著運動app和手環的普及和應用,在朋友圈、運動圈中出現了每天1萬步的健身打卡現象,“日行一萬步,健康一輩子”的觀念廣泛流傳.“健步達人”小王某天統計了他朋友圈中所有好友(共500人)的走路步數,并整理成下表:
分組(單位:千步) |
|
|
|
|
|
|
|
|
頻數 | 60 | 240 | 100 | 60 | 20 | 18 | 0 | 2 |
(1)請估算這一天小王朋友圈中好友走路步數的平均數(同一組中數據以這組數據所在區間中點值作代表);
(2)若用![]() 表示事件“走路步數低于平均步數”,試估計事件
表示事件“走路步數低于平均步數”,試估計事件![]() 發生的概率;
發生的概率;
(3)若稱每天走路不少于8千步的人為“健步達人”,小王朋友圈中歲數在40歲以上的中老年人共有300人,其中健步達人恰有150人,請填寫下面![]() 列聯表.根據列聯表判斷,有多大把握認為,健步達人與年齡有關?
列聯表.根據列聯表判斷,有多大把握認為,健步達人與年齡有關?
健步達人 | 非健步達人 | 合計 | |
40歲以上 | |||
不超過40歲 | |||
合計 |
附: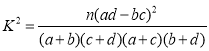 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)![]() ;(2)0.6216;(3)見解析.
;(2)0.6216;(3)見解析.
【解析】
(1)由數據和平均值的計算公式可得答案,(2)由頻率估計概率可得答案,(3)根據題目所給的數據填寫2×2列聯表即可,計算K2,對照題目中的表格,得出統計結論.
(1)由題意可得這一天小王朋友圈中好友走路步數的平均數為:![]() ,
,
所以這一天小王500名好友走路的平均步數約為8.432步.
(2)由頻率約等概率可得:![]() ,
,
所以事件A的概率約為0.6216.
(3)根據題目所給的數據填寫2×2列聯表如下:
健步達人 | 非健步達人 | 合計 | |
40歲以上 | 150 | 150 | 300 |
不超過40歲 | 50 | 150 | 200 |
合計 | 200 | 300 | 500 |
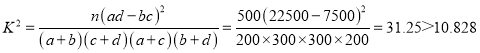 ,
,
∴有99.9%以上的把握認為,健步達人與年齡有關.


科目:高中數學 來源: 題型:
【題目】11月,2019全國美麗鄉村籃球大賽在中國農村改革的發源地-安徽鳳陽舉辦,其間甲、乙兩人輪流進行籃球定點投籃比賽(每人各投一次為一輪),在相同的條件下,每輪甲乙兩人在同一位置,甲先投,每人投一次球,兩人有1人命中,命中者得1分,未命中者得-1分;兩人都命中或都未命中,兩人均得0分,設甲每次投球命中的概率為![]() ,乙每次投球命中的概率為
,乙每次投球命中的概率為![]() ,且各次投球互不影響.
,且各次投球互不影響.
(1)經過1輪投球,記甲的得分為![]() ,求
,求![]() 的分布列;
的分布列;
(2)若經過![]() 輪投球,用
輪投球,用![]() 表示經過第
表示經過第![]() 輪投球,累計得分,甲的得分高于乙的得分的概率.
輪投球,累計得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②規定![]() ,經過計算機計算可估計得
,經過計算機計算可估計得![]() ,請根據①中
,請根據①中![]() 的值分別寫出a,c關于b的表達式,并由此求出數列
的值分別寫出a,c關于b的表達式,并由此求出數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
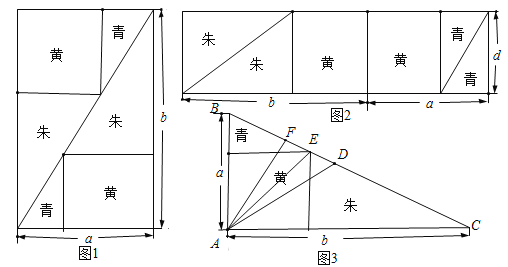
【題目】《九章算術》中“勾股容方”問題:“今有勾五步,股十二步,問勾中容方幾何?”魏晉時期數學家劉徽在其《九章算術注》中利用出入相補原理給出了這個問題的一般解法:如圖1,用對角線將長和寬分別為![]() 和
和![]() 的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為
的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為![]() ,寬為內接正方形的邊長
,寬為內接正方形的邊長![]() .由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設
.由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設![]() 為斜邊
為斜邊![]() 的中點,作直角三角形
的中點,作直角三角形![]() 的內接正方形對角線
的內接正方形對角線![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則下列推理正確的是( )
,則下列推理正確的是( )
①由圖1和圖2面積相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得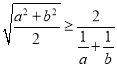 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=BC=1,∠ABC=60°,四邊形ACFE為矩形,平面ACFE⊥平面ABCD,CF=1.
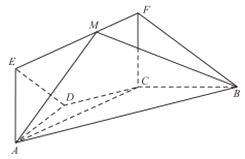
(1)證明:BC⊥平面ACFE;
(2)設點M在線段EF上運動,平面MAB與平面FCB所成銳二面角為θ,求cosθ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對有![]() 個元素的總體
個元素的總體![]() 進行抽樣,先將總體分成兩個子總體
進行抽樣,先將總體分成兩個子總體![]() 和
和![]() (
(![]() 是給定的正整數,且
是給定的正整數,且![]() ),再從每個子總體中各隨機抽取2個元素組成樣本.用
),再從每個子總體中各隨機抽取2個元素組成樣本.用![]() 表示元素
表示元素![]() 和
和![]() 同時出現在樣本中的概率.
同時出現在樣本中的概率.
(1)求![]() 的表達式(用
的表達式(用![]() ,
,![]() 表示);
表示);
(2)求所有![]() 的和.
的和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,當
,當![]() 時
時![]() ,則關于函數
,則關于函數![]() 有如下四個結論:①
有如下四個結論:①![]() 為偶函數;②
為偶函數;②![]() 的圖象關于直線
的圖象關于直線![]() 對稱;③方程
對稱;③方程![]() 有兩個不等實根;④
有兩個不等實根;④![]() 其中所有正確結論的編號是_______.
其中所有正確結論的編號是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com