【題目】已知在
中，角
的對邊分別為
,且
.
（1）求
的值；
（2）若
,求
的取值范圍.
【答案】（1）
（2）
【解析】試題分析：（1）本問考查解三角形中的的“邊角互化”.由于求
的值，所以可以考慮到根據余弦定理將
分別用邊表示，再根據正弦定理可以將
轉化為
，于是可以求出的值；（2）首先根據
求出角
的值，根據第（1）問得到的值，可以運用正弦定理求出
外接圓半徑
，于是可以將
轉化為
，又因為角的值已經得到，所以將轉化為關于
的正弦型函數表達式，這樣就可求出取值范圍；另外本問也可以在求出角的值后，應用余弦定理及重要不等式
，求出的最大值，當然，此時還要注意到三角形兩邊之和大于第三邊這一條件.
試題解析：（1）由
，
應用余弦定理，可得
化簡得
則
（2）
![](http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/13/f1846313/SYS201712291335548994926602_DA/SYS201712291335548994926602_DA.020.png"){kind=small}
即
所以
法一. 
,
則
=
=
=
又
法二
因為 由余弦定理
得
，
又因為
，當且僅當
時“
”成立.
所以 
又由三邊關系定理可知
綜上
名師點睛字詞句段篇系列答案科目：高中數學 來源： 題型：
【題目】已知函數
，其中常數
．
（Ⅰ）當
，求函數
的單調遞增區間；
（Ⅱ）設定義在
上的函數
在點
處的切線方程為
， 若
在
內恒成立，則稱
為函數
的“類對稱點”，當
時，試問
是否存在“類對稱點”，若存在，請求出一個“類對稱點”的橫坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
的定義域是
，對于以下四個命題：
(1) 若
是奇函數，則
也是奇函數；
(2) 若
是周期函數，則
也是周期函數；
(3) 若
是單調遞減函數，則
也是單調遞減函數；
(4) 若函數
存在反函數
，且函數
有零點，則函數
也有零點．
其中正確的命題共有
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數 
是定義在（﹣1，1）上的奇函數，且 
．
（1）確定函數的解析式；
（2）證明函數f（x）在（﹣1，1）上是增函數；
（3）解不等式f（t﹣1）+f（t）＜0．
查看答案和解析>>
科目：高中數學 來源： 題型：
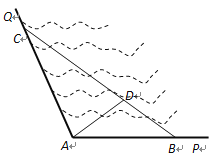
【題目】如圖所示， 
是某海灣旅游區的一角，其中
，為了營造更加優美的旅游環境，旅游區管委會決定在直線海岸
和
上分別修建觀光長廊
和AC，其中
是寬長廊，造價是
元/米， 
是窄長廊，造價是
元/米，兩段長廊的總造價為120萬元，同時在線段
上靠近點
的三等分點
處建一個觀光平臺，并建水上直線通道
（平臺大小忽略不計），水上通道的造價是
元/米．
(1) 若規劃在三角形
區域內開發水上游樂項目，要求
的面積最大，那么
和
的長度分別為多少米？
(2) 在(1)的條件下，建直線通道
還需要多少錢？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（cosα，sinα）， 
=（cosβ，sinβ），| ﹣ |= 
．
（1）求cos（α﹣β）的值；
（2）若﹣ 
＜β＜0＜α＜ ，且sinβ=﹣ 
，求sinα的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sinx+sin（x+ 
），x∈R．
（1）求f（x）的最小正周期；
（2）求f（x）的最大值和最小值；
（3）若f（α）= 
，求sin 2α的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，曲線
在點
處的切線與直線
垂直（其中
為自然對數的底數）．
（I）求
的解析式及單調遞減區間；
（II）是否存在常數
，使得對于定義域內的任意
恒成立？若存在，求出
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
是圓心為
的圓
上的動點，點
， 
為坐標原點，線段
的垂直平分線交
于點
.
（1）求動點
的軌跡
的方程；
（2）過原點
作直線
交（1）中的軌跡
于點
，點
在軌跡
上，且
，點
滿足
，試求四邊形
的面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com