
【題目】在四棱錐![]() 中,四邊形
中,四邊形![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析(2) ![]()
【解析】試題分析:
(1)連接![]() 交
交![]() 于點
于點![]() ,則
,則![]() 為
為![]() 的中點,連接
的中點,連接![]() .由三角形中位線的性質可得
.由三角形中位線的性質可得![]() ,結合線面平行的判斷定理可得
,結合線面平行的判斷定理可得![]() 平面
平面![]() .
.
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() .由幾何關系可證得
.由幾何關系可證得![]() 平面
平面![]() .且
.且![]() ,則
,則![]()
![]() .在
.在![]() 中,由余弦定理可得
中,由余弦定理可得![]()
![]() .由勾股定理可得
.由勾股定理可得![]() ,則等腰
,則等腰![]() 的面積為
的面積為![]() ,設點
,設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,利用體積相等列方程可得點
,利用體積相等列方程可得點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
試題解析:
(1)連接![]() 交
交![]() 于點
于點![]() ,
,
則![]() 為
為![]() 的中點,連接
的中點,連接![]() .
.
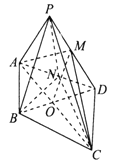
在![]() 中,
中, ![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
由余弦定理,得![]()
![]() .
.
∴![]() ,
,
∴![]() 的面積為
的面積為 ,
,
設點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() .
.
即點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】甲乙兩地相距![]() 海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為
海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為![]() ,其他費用為每小時
,其他費用為每小時![]() 元,且該貨輪的最大航行速度為
元,且該貨輪的最大航行速度為![]() 海里/小時.
海里/小時.
(![]() )請將該貨輪從甲地到乙地的運輸成本
)請將該貨輪從甲地到乙地的運輸成本![]() 表示為航行速度
表示為航行速度![]() (海里/小時)的函數.
(海里/小時)的函數.
(![]() )要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
)要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() :
: ![]() 經過伸縮變換
經過伸縮變換![]() 后得到曲線
后得到曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求出曲線![]() 、
、![]() 的參數方程;
的參數方程;
(Ⅱ)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 、
、![]() 上的動點,求
上的動點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E、F分別是BC、CD的中點,G是EF的中點,現在沿AE、AF及EF把這個正方形折成一個空間圖形,使B、C、D三點重合,重合后的點記為H,那么,在這個空間圖形中必有( )
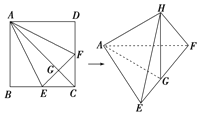
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩名運動員互不影響地進行四次設計訓練,根據以往的數據統計,他們設計成績均不低于8環(成績環數以整數計),且甲乙射擊成績(環數)的分布列如下:
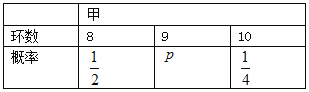
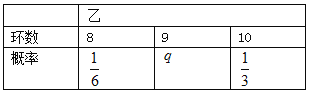
(I)求![]() ,
, ![]() 的值;
的值;
(II)若甲乙兩射手各射擊兩次,求四次射擊中恰有三次命中9環的概率;
(III)若兩個射手各射擊1次,記兩人所得環數的差的絕對值為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
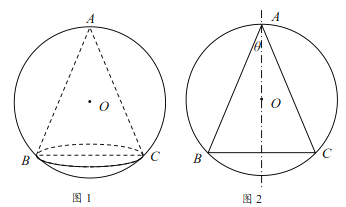
【題目】某藝術品公司欲生產一款迎新春工藝禮品,該禮品是由玻璃球面和該球的內接圓錐組成,圓錐的側面用于藝術裝飾,如圖1.為了便于設計,可將該禮品看成是由圓![]() 及其內接等腰三角形
及其內接等腰三角形![]() 繞底邊
繞底邊![]() 上的高所在直線
上的高所在直線![]() 旋轉180°而成,如圖2.已知圓
旋轉180°而成,如圖2.已知圓![]() 的半徑為
的半徑為![]() ,設
,設![]() ,圓錐的側面積為
,圓錐的側面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)為了達到最佳觀賞效果,要求圓錐的側面積![]() 最大.求
最大.求![]() 取得最大值時腰
取得最大值時腰![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
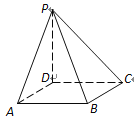
【題目】在四棱錐P–ABCD中,底面ABCD是邊長為6的正方形,PD平面ABCD,PD=8.
(1) 求PB與平面ABCD所成角的大小;
(2) 求異面直線PB與DC所成角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com