
分析 利用正弦函數的性質,即可求得函數y=2sin(3x+$\frac{π}{4}$)的定義域、最小正周期、值域、單調性.
解答 解:函數y=2sin(3x+$\frac{π}{4}$)的定義域為R;
∵-1≤sin(3x+$\frac{π}{4}$)≤1,
∴-2≤2sin(3x+$\frac{π}{4}$)≤2,
∴函數y=2sin(3x+$\frac{π}{4}$)的值域為:[-2,2];
最小正周期T=$\frac{2π}{3}$,
由2kπ-$\frac{π}{2}$≤3x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$(k∈Z)得:$\frac{2}{3}$kπ-$\frac{π}{4}$≤x≤$\frac{2}{3}$kπ+$\frac{π}{12}$(k∈Z),
∴函數y=2sin(3x+$\frac{π}{4}$)的單調增區間為[$\frac{2}{3}$kπ-$\frac{π}{4}$,$\frac{2}{3}$kπ+$\frac{π}{12}$](k∈Z);
由2kπ+$\frac{π}{2}$≤3x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$(k∈Z)得:$\frac{2}{3}$kπ+$\frac{π}{12}$≤x≤$\frac{2}{3}$kπ+$\frac{5π}{12}$(k∈Z),
∴函數y=2sin(3x+$\frac{π}{4}$)的單調減區間為[$\frac{2}{3}$kπ+$\frac{π}{12}$,$\frac{2}{3}$kπ+$\frac{5π}{12}$](k∈Z).
點評 本題考查正弦函數的性質,著重考查其定義域、最小正周期、值域、單調性,屬于基礎題.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | M>N | B. | M<N | C. | M≥N | D. | M≤N |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
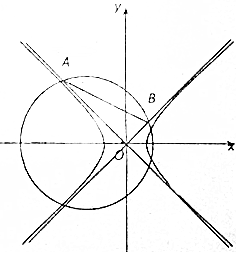 如圖,雙曲線k2x2-y2=1(k>0)的兩條漸近線與圓(x+2)2+y2=5在x軸的上方交于A、B兩點.
如圖,雙曲線k2x2-y2=1(k>0)的兩條漸近線與圓(x+2)2+y2=5在x軸的上方交于A、B兩點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,+∞) | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com