【題目】已知函數
.
（Ⅰ）求函數
的單調區間；
（Ⅱ）若函數
存在極小值點
，且
，求實數
的取值范圍.
【答案】（Ⅰ）當
時，函數
的單調遞減區間為
；當
時，函數
的單調遞增區間為
，單調遞減區間為
；（Ⅱ） 
.
【解析】試題分析：（Ⅰ）求出
， 分兩種情況分別令
得增區間， 
得減區間；（Ⅱ）函數
存在極小值點，所以
在
上存在兩個零點
， 
，設
為函數
的極小值點
，由
，得
，所以
可得結果.
試題解析：（Ⅰ）因為函數
，所以其定義域為
.
所以
.
當
時， 
，函數
在區間
上單調遞減.
當
時， 
.
當
時， 
，函數
在區間
上單調遞減.
當
時， 
，函數
在區間
上單調遞增.
綜上可知，當
時，函數
的單調遞減區間為
；當
時，函數
的單調遞增區間為
，單調遞減區間為
.
（Ⅱ）因為
，
所以
（
）.
因為函數
存在極小值點，所以
在
上存在兩個零點
， 
，且
.
即方程
的兩個根為
， 
，且
，
所以
，解得
.
則
.
當
或
時， 
，當
時， 
，
所以函數
的單調遞減區間為
與
，單調遞增區間為
.
所以
為函數
的極小值點
.
由
，得
.
由于
等價于
.
由
，得
，所以
.
因為
，所以有
，即
.
因為
，所以
.
解得
.
所以實數
的取值范圍為
.
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和Sn=3n+m（m為常數，n∈N+）
（1）求a1 ， a2 ， a3；
（2）若數列{an}為等比數列，求常數m的值及an；
（3）對于（2）中的an ， 記f（n）=λa2n+1﹣4λan+1﹣7，若f（n）＜0對任意的正整數n恒成立，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心在
軸上的圓
與直線
切于點
.
（1）求圓
的標準方程；
（2）已知
，經過原點，且斜率為正數的直線
與圓
交于
兩點.
（ⅰ）求證： 
為定值；
（ⅱ）求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
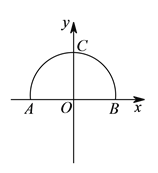
【題目】如圖是一段圓錐曲線，曲線與兩個坐標軸的交點分別是
， 
， 
.
（Ⅰ）若該曲線表示一個橢圓，設直線
過點
且斜率是
，求直線
與這個橢圓的公共點的坐標.
（Ⅱ）若該曲線表示一段拋物線，求該拋物線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，以坐標原點
為極點， 
軸正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為： 
，直線
的參數方程是
（
為參數， 
）．
（1）求曲線
的直角坐標方程；
（2）設直線
與曲線
交于兩點
，且線段
的中點為
，求
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學數學老師分別用兩種不同教學方式對入學數學平均分和優秀率都相同的甲、乙兩個高一新班（人數均為20人）進行教學（兩班的學生學習數學勤奮程度和自覺性一致），數學期終考試成績莖葉圖如下：
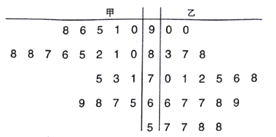
（1）學校規定：成績不低于75分的為優秀，請填寫下面的
聯表，并判斷有多大把握認為“成績優秀與教學方式有關”．
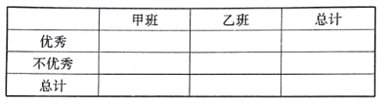
附：參考公式及數據
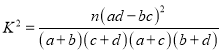
（2）從兩個班數學成績不低于90分的同學中隨機抽取3名，設
為抽取成績不低于95分同學人數，求
的分布列和期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某網站針對2015年中國好聲音歌手A，B，C三人進行網上投票，結果如下
觀眾年齡 | 支持A | 支持B | 支持C |
20歲以下 | 100 | 200 | 600 |
20歲以上（含20歲） | 100 | 100 | 400 |
（1）在所有參與該活動的人中，用分層抽樣的方法抽取n人，其中有6人支持A，求n的值．
（2）在支持C的人中，用分層抽樣的方法抽取5人作為一個總體，從這5人中任意選取2人，求恰有1人在20歲以下的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面內有向量 
=（1，7）， 
=（5，1）， 
=（2，1），點X為直線OP上的一個動點．
（1）當 
取最小值時，求 
的坐標；
（2）當點X滿足（1）的條件和結論時，求cos∠AXB的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
