
【題目】某學校在平面圖為矩形的操場ABCD內(nèi)進行體操表演,其中AB=40,BC=15,O為AB上一點,且BO=10,線段OC、OD、MN為表演隊列所在位置(M、N分別在線段OD、OC上),△OCD內(nèi)的點P為領(lǐng)隊位置,且P到OC、OD的距離分別為![]() 、
、![]() ,記OM=d,我們知道當△OMN面積最小時觀賞效果最好.
,記OM=d,我們知道當△OMN面積最小時觀賞效果最好.
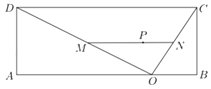
(1)當d為何值時,P為隊列MN的中點;
(2)怎樣安排M的位置才能使觀賞效果最好?求出此時△OMN的面積.
【答案】(1)![]() .(2) M,N,P 三點共線,面積為
.(2) M,N,P 三點共線,面積為![]() .
.
【解析】
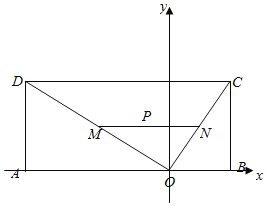
1)以O為坐標原點,AB所在直線為x軸,過O垂直于AB的直線為y軸,建立如圖所示的平面直角坐標系,OC:y=1.5x;OD:y=﹣0.5x,設(shè)P(a,b),M(﹣2m,m),N(n,1.5n),(m>0,n>0),求解即可
(2)通過![]() 推出
推出![]() ,利用基本不等式以及三角形面積公式即可
,利用基本不等式以及三角形面積公式即可
(1)以O為坐標原點,AB所在直線為x軸,過O垂直于AB的直線為y軸,建立如圖所示的平面直角坐標系.則C(10,15),B(10,0),D(﹣30,15),P(﹣4,4).OC:y=1.5x;OD:y=﹣0.5x,
設(shè)P(a,b),M(﹣2m,m),N(n,1.5n),(m>0,n>0),
P到OC、OD的距離分別為![]() 、
、![]() ,聯(lián)立解方程組
,聯(lián)立解方程組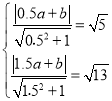 ,得
,得![]() ,
,
∵P為MN的中點,所以![]() ,得m
,得m![]() ,n
,n![]() ,所以
,所以![]() ,
,
∴d=|OM|![]() .
.
(2)由M,N,P 三點共線,得![]() ,5m+6.5n=4mn,即
,5m+6.5n=4mn,即![]() ,
,
S△OMN![]() ,
,
(2m+n)![]() ,當且僅當5n2=13m2成立,
,當且僅當5n2=13m2成立,
所以△OMN面積最小為![]() .
.


 一課一練課時達標系列答案
一課一練課時達標系列答案科目:高中數(shù)學 來源: 題型:
【題目】以下四個命題:
①“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
②“![]() ”是“函數(shù)
”是“函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù)”的充分不必要條件
上為增函數(shù)”的充分不必要條件
③若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為假命題
均為假命題
④對于命題![]() :
:![]() ,
,![]() ,則
,則![]() 為:
為:![]() ,
,![]()
其中真命題的個數(shù)是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,定義橢圓
,定義橢圓![]() 上的點
上的點![]() 的“伴隨點”為
的“伴隨點”為![]() .
.
(1)求橢圓![]() 上的點
上的點![]() 的“伴隨點”
的“伴隨點”![]() 的軌跡方程;
的軌跡方程;
(2)如果橢圓![]() 上的點
上的點![]() 的“伴隨點”為
的“伴隨點”為![]() ,對于橢圓
,對于橢圓![]() 上的任意點
上的任意點![]() 及它的“伴隨點”
及它的“伴隨點”![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
, ![]() 時,直線
時,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,若點
兩點,若點![]() ,
, ![]() 的“伴隨點”分別是
的“伴隨點”分別是![]() ,
, ![]() ,且以
,且以![]() 為直徑的圓經(jīng)過坐標原點
為直徑的圓經(jīng)過坐標原點![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
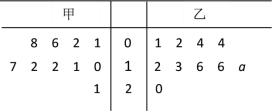
【題目】為培養(yǎng)學生的閱讀習慣,某校開展了為期一年的“弘揚傳統(tǒng)文化,閱讀經(jīng)典名著”活動. 活動后,為了解閱讀情況,學校統(tǒng)計了甲、乙兩組各10名學生的閱讀量(單位:本),統(tǒng)計結(jié)果用莖葉圖記錄如下,乙組記錄中有一個數(shù)據(jù)模糊,無法確認,在圖中以a表示.
(Ⅰ)若甲組閱讀量的平均值大于乙組閱讀量的平均值, 求圖中a的所有可能取值;
(Ⅱ)將甲、乙兩組中閱讀量超過15本的學生稱為“閱讀達人”. 設(shè)![]() ,現(xiàn)從所有“閱讀達人”里任取3人,求其中乙組的人數(shù)X的分布列和數(shù)學期望.
,現(xiàn)從所有“閱讀達人”里任取3人,求其中乙組的人數(shù)X的分布列和數(shù)學期望.
(Ⅲ)記甲組閱讀量的方差為![]() . 在甲組中增加一名學生A得到新的甲組,若A的閱讀量為10,則記新甲組閱讀量的方差為
. 在甲組中增加一名學生A得到新的甲組,若A的閱讀量為10,則記新甲組閱讀量的方差為![]() ;若A的閱讀量為20,則記新甲組閱讀量的方差為
;若A的閱讀量為20,則記新甲組閱讀量的方差為![]() ,試比較
,試比較![]() ,
,![]() ,
,![]() 的大小.(結(jié)論不要求證明)
的大小.(結(jié)論不要求證明)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】團體購買公園門票,票價如下表:
購票人數(shù) | 1~50 | 51~100 | 100以上 |
門票價格 | 13元/人 | 11元/人 | 9元/人 |
現(xiàn)某單位要組織其市場部和生產(chǎn)部的員工游覽該公園,這兩個部門人數(shù)分別為a和b![]() ,若按部門作為團體,選擇兩個不同的時間分別購票游覽公園,則共需支付門票費為1290元;若兩個部門合在一起作為一個團體,同一時間購票游覽公園,則需支付門票費為990元,那么這兩個部門的人數(shù)
,若按部門作為團體,選擇兩個不同的時間分別購票游覽公園,則共需支付門票費為1290元;若兩個部門合在一起作為一個團體,同一時間購票游覽公園,則需支付門票費為990元,那么這兩個部門的人數(shù)![]() ____;
____;![]() ____.
____.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在多面體![]() 中,底面
中,底面![]() 為矩形,側(cè)面
為矩形,側(cè)面![]() 為梯形,
為梯形,![]() ,
,![]() ,
,![]() .
.
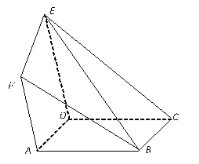
(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)判斷線段![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?并說明理由.
?并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某中學為了組建一支業(yè)余足球隊,在高一年級隨機選取50名男生測量身高,發(fā)現(xiàn)被測男生的身高全部在![]() 到
到![]() 之間,將測量結(jié)果按如下方式分成六組:第1組
之間,將測量結(jié)果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,…,第6組
,…,第6組![]() ,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
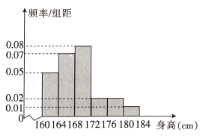
(1)若學校要從中選1名男生擔任足球隊長,求被選取的男生恰好在第5組或第6組的概率;
(2)試估計該校高一年級全體男生身高的平均數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點值代表)與中位數(shù);
(3)現(xiàn)在從第5與第6組男生中選取兩名同學擔任守門員,求選取的兩人中最多有1名男生來自第5組的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 是自然對數(shù)的底數(shù),函數(shù)
是自然對數(shù)的底數(shù),函數(shù)![]() 與
與![]() 的定義域都是
的定義域都是![]() .
.
(1)求函數(shù)![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求證:函數(shù)![]() 只有一個零點
只有一個零點![]() ,且
,且![]() ;
;
(3)用![]() 表示
表示![]() ,
,![]() 的最小值,設(shè)
的最小值,設(shè)![]() ,
,![]() ,若函數(shù)
,若函數(shù)![]() 在
在![]() 上為增函數(shù),求實數(shù)
上為增函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com