
【題目】已知函數![]()
(1)若![]() 是
是![]() 的極值點,求
的極值點,求![]() 的極大值;
的極大值;
(2)求實數![]() 的范圍,使得
的范圍,使得![]() 恒成立.
恒成立.
【答案】(1)![]() 的極大值為
的極大值為![]() ;(2)
;(2)![]() 時,
時,![]() 恒成立.
恒成立.
【解析】試題分析:(1)由于x=2是f(x)的極值點,則f′(3)=0求出a,進而求出f′(x)>0得到函數的增區間,求出f′(x)<0得到函數的減區間,即可得到函數的極大值;
(2)由于f(x)≥1恒成立,即x>0時,![]() x2﹣(a+1)x+alnx≥0恒成立,設g(x)=
x2﹣(a+1)x+alnx≥0恒成立,設g(x)=![]() x2﹣(a+1)x+alnx,求出函數的導數,分類討論參數a,得到函數g(x)的最小值≥0,即可得到a的范圍.
x2﹣(a+1)x+alnx,求出函數的導數,分類討論參數a,得到函數g(x)的最小值≥0,即可得到a的范圍.
(1) ![]()
![]() 是
是![]() 的極值點,
的極值點,![]() 解得
解得![]()
當![]() 時,
時,![]()
當![]() 變化時,
變化時,

![]() 的極大值為
的極大值為![]()
(2)要使得![]() 恒成立,即
恒成立,即![]() 時,
時,![]() 恒成立,
恒成立,
設![]() ,則
,則![]() ,
,
(ⅰ)當![]() 時,由
時,由![]() 得函數
得函數![]() 單調減區間為
單調減區間為![]() ,由
,由![]() 得函數
得函數![]() 單調增區間為
單調增區間為![]() ,此時
,此時![]() ,得
,得![]()
(ⅱ)當![]() 時,由
時,由![]() 得函數
得函數![]() 單調減區間為
單調減區間為![]() ,由
,由![]() 得函數
得函數![]() 單調增區間為
單調增區間為![]() ,此時
,此時![]() 不合題意.
不合題意.
(ⅲ)當![]() 時,
時,![]() 在
在![]() 上單調遞增,此時
上單調遞增,此時![]() 不合題意
不合題意
(ⅳ)當![]() 時,由
時,由![]() 得函數
得函數![]() 單調減區間為
單調減區間為![]() ,由
,由![]() 得函數
得函數![]() 單調增區間為
單調增區間為![]() ,此時
,此時![]() 不合題意.
不合題意.
綜上所述:![]() 時,
時,![]() 恒成立.
恒成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥底面ABCD,底面ABCD為正方形,PD=DC,E,F分別是AB,PB的中點 
(1)求證:EF⊥CD;
(2)在平面PAD內求一點G,使GF⊥平面PCB,并證明你的結論;
(3)求DB與平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的周長為l,面積為S,則△ABC的內切圓半徑為r= ![]() .將此結論類比到空間,已知四面體ABCD的表面積為S,體積為V,則四面體ABCD的內切球的半徑R= .
.將此結論類比到空間,已知四面體ABCD的表面積為S,體積為V,則四面體ABCD的內切球的半徑R= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩千多年前,古希臘畢達哥拉斯學派的數學家曾經在沙灘上研究數學問題.他們在沙灘上畫點或用小石子表示數,按照點或小石子能排列的形狀對數進行分類.如下圖中實心點的個數5,9,14,20,…為梯形數.根據圖形的構成,記此數列的第2013項為a2013 , 則a2013﹣5=( ) 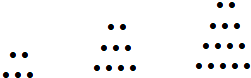
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足f(x)+f(x+5)=16,當x∈(﹣1,4]時,f(x)=x2﹣2x , 則函數f(x)在區間[0,2016]上的零點個數是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】歐陽修《賣油翁)中寫到:“(翁)乃取一葫蘆置于地,以錢覆其口,徐以杓酌漓瀝之,自錢孔入,而錢不濕”,可見“行行出狀元”,賣油翁的技藝讓人嘆為觀止,若銅錢是直徑為4 cm的圓,中間有邊長為l cm的正方形孔.若隨機向銅錢上滴一滴油(設油滴整體落在銅錢上).則油滴(設油滴是直徑為0.2 cm的球)正好落入孔中(油滴整體落入孔中)的概率是_________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先后擲子(子的六個面上分別標有1,2,3,4,5,6個點)兩次,落在水平桌面后,記正面朝上的點數分別為x,y,設事件A為“x+y為偶數”,事件B為“x,y中有偶數且x≠y”,則概率P(B|A)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,且滿足a1=2,Sn-4Sn-1-2=0(n≥2,n∈Z).
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)令bn=log2an,Tn為{bn}的前n項和,求證![]() <2.
<2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com