
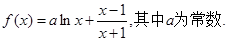
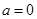 ,求曲線
,求曲線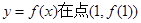 處的切線方程;
處的切線方程; 的單調(diào)性.
的單調(diào)性. .
. 時,函數(shù)
時,函數(shù) 在
在 上單調(diào)遞增;
上單調(diào)遞增; 時,函數(shù)
時,函數(shù) 在
在 上單調(diào)遞減;
上單調(diào)遞減; 時,
時, 在
在 ,
, 上單調(diào)遞減,
上單調(diào)遞減, 上單調(diào)遞增.
上單調(diào)遞增.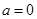 時,
時, ,求切線的斜率,即
,求切線的斜率,即 ,又
,又 ,由直線方程的點斜式進一步整理,得到切線方程為
,由直線方程的點斜式進一步整理,得到切線方程為 .
. 的定義域為
的定義域為 ,
, ,根據(jù)
,根據(jù) 的不同情況,討論導(dǎo)函數(shù)值的正負,以確定函數(shù)的單調(diào)性.其中
的不同情況,討論導(dǎo)函數(shù)值的正負,以確定函數(shù)的單調(diào)性.其中 時,情況較為單一,
時,情況較為單一, ,函數(shù)
,函數(shù) 在
在 上單調(diào)遞增,
上單調(diào)遞增, 時,令
時,令 ,
, ,再分
,再分 ,
, ,
, 等情況加以討論.
等情況加以討論.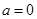 時,
時, ,
, ,
, ,又
,又 ,
, 在
在 處的切線方程為
處的切線方程為 .
. 的定義域為
的定義域為 ,
, ,
, 時,
時, ,函數(shù)
,函數(shù) 在
在 上單調(diào)遞增,
上單調(diào)遞增, 時,令
時,令 ,
, ,
, 時,
時, ,
, ,函數(shù)
,函數(shù) 在
在 上單調(diào)遞減,
上單調(diào)遞減, 時,
時, ,
, ,函數(shù)
,函數(shù) 在
在 上單調(diào)遞減,
上單調(diào)遞減, 時,
時, ,
, 是函數(shù)
是函數(shù) 的兩個零點,
的兩個零點, ,
, ,
,
 ,
, 時,
時, ,函數(shù)
,函數(shù) 單調(diào)遞減,
單調(diào)遞減, 時,
時, ,函數(shù)
,函數(shù) 單調(diào)遞增,
單調(diào)遞增, 時,
時, ,函數(shù)
,函數(shù) 單調(diào)遞減,
單調(diào)遞減, 時,函數(shù)
時,函數(shù) 在
在 上單調(diào)遞增;
上單調(diào)遞增; 時,函數(shù)
時,函數(shù) 在
在 上單調(diào)遞減;
上單調(diào)遞減; 時,
時, 在
在 ,
, 上單調(diào)遞減,
上單調(diào)遞減, 上單調(diào)遞增.
上單調(diào)遞增.

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
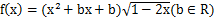 .
.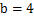 時,求
時,求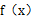 的極值;
的極值;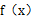 在區(qū)間
在區(qū)間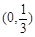 上單調(diào)遞增,求b的取值范圍.
上單調(diào)遞增,求b的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 ,且對任意實數(shù)x,總有
,且對任意實數(shù)x,總有 /(x)<3
/(x)<3 <3x-15的解集為( )
<3x-15的解集為( )| A.(﹣∞,4) |
| B.(﹣∞,﹣4) |
| C.(﹣∞,﹣4)∪(4,﹢∞) |
| D.(4,﹢∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
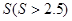 平方米的矩形場地的圍墻,要求在前面墻的正中間留一個寬度為2米的出入口,后面墻長度不超過20米,已知后面墻的造價為每米45元,其它墻的造價為每米180元,設(shè)后面墻長度為x米,修建此矩形場地圍墻的總費用為
平方米的矩形場地的圍墻,要求在前面墻的正中間留一個寬度為2米的出入口,后面墻長度不超過20米,已知后面墻的造價為每米45元,其它墻的造價為每米180元,設(shè)后面墻長度為x米,修建此矩形場地圍墻的總費用為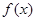 元.
元.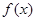 的表達式;
的表達式;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com