Question

用向量法證明三角形的三條高線交于一點.

Answer 1

思路分析：可設(shè)兩條高線交于一點,只要證明第三條高也過此點即可.

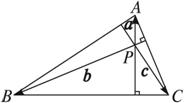
證明：如圖,設(shè)△ABC的BC、CA兩邊上的高交于點P.再證PC⊥AB.

設(shè)=a,=b,=c,則=b-a,=c-b, =a-c.

∵⊥,⊥,

∴a·(c-b)=0,

即a·c=a·b;b·(a-c)=0,

即a·b=b·c.

從而a·c=b·c,

即c·(b-a)=0.

所以⊥,即PC⊥AB.

這就證明了點P在△ABC的第三邊AB的高線上,所以△ABC的三條高線交于一點.

方法歸納 證明三線共點,常變換思維方式,以減少思維量.對于垂直這種特殊情況常先借助向量垂直的充要條件,再進一步進行向量運算來解決問題.